
【题目】已知,椭圆C过点A ![]() ,两个焦点为(﹣1,0),(1,0).
,两个焦点为(﹣1,0),(1,0).
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
【答案】
(1)解:由题意,c=1,
可设椭圆方程为 ![]() ,
,
解得b2=3, ![]() (舍去)
(舍去)
所以椭圆方程为 ![]()
(2)解:设直线AE方程为: ![]() ,
,
代入 ![]() 得
得 ![]()
设E(xE,yE),F(xF,yF),
因为点 ![]() 在椭圆上,
在椭圆上,
所以由韦达定理得: ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() .
.
又直线AF的斜率与AE的斜率互为相反数,
在上式中以﹣K代K,可得 ![]() ,
, ![]()
所以直线EF的斜率 ![]()
即直线EF的斜率为定值,其值为 ![]()
【解析】(1)由题意,c=1,可设椭圆方程代入已知条件得 ![]() ,求出b,由此能够求出椭圆方程.(2)设直线AE方程为:
,求出b,由此能够求出椭圆方程.(2)设直线AE方程为: ![]() ,代入
,代入 ![]() 得
得 ![]() ,再点
,再点 ![]() 在椭圆上,结合直线的位置关系进行求解.
在椭圆上,结合直线的位置关系进行求解.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣8≤0,x∈R},B={x|x2﹣(2m﹣3)x+m2﹣3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() ,
, ![]() 的夹角为60°且|
的夹角为60°且| ![]() |=|
|=| ![]() |=1,如果
|=1,如果 ![]() ,
, ![]() ,
, ![]() .
.
(1)证明:A、B、D三点共线.
(2)试确定实数k的值,使k的取值满足向量 ![]() 与向量
与向量 ![]() 垂直.
垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =3
=3 ![]() 1﹣2
1﹣2 ![]() 2 ,
2 , ![]() =4
=4 ![]() 1+
1+ ![]() 2 , 其中
2 , 其中 ![]() 1=(1,0),
1=(1,0), ![]() 2=(0,1),求:
2=(0,1),求:
(1)![]()
![]() 和|
和| ![]() +
+ ![]() |的值;
|的值;
(2)![]() 与
与 ![]() 夹角θ的余弦值.
夹角θ的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若(a+b+c)(b+c﹣a)=3ab,且sinA=2sinBcosC,那么△ABC是( )
A.直角三角形
B.等边三角形
C.等腰三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校伙食长期以面粉和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米食每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠BAD=90°,AD= ![]() ,DC=2AB=2,E为BC中点.
,DC=2AB=2,E为BC中点. 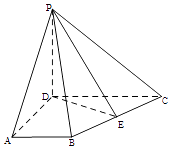
(1)求证:平面PBC⊥平面PDE
(2)线段PC上是否存在一点F,使PA∥平面BDF?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在斜三棱柱ABC﹣A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在面ABC上的射影H必在( ) 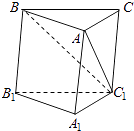
A.直线AB上
B.直线BC上
C.直线CA上
D.△ABC内部
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com