
分析 根据直线与圆没有公共点得到直线与圆的位置关系是相离,则根据圆心到直线的距离大于半径列出关于a的不等式,解不等式即可得到a的范围.
解答 解:把圆x2+y2-2x=0化为标准方程为(x-1)2+y2=1,所以圆心(1,0),半径r=1,
由直线与圆没有公共点得到:圆心(1,0)到直线2x-y+a=0距离d=$\frac{|2+a|}{\sqrt{4+1}}$>r=1,
∴|a+2|>$\sqrt{5}$
∴a<-2-$\sqrt{5}$或a>-2+$\sqrt{5}$
故答案为:a<-2-$\sqrt{5}$或a>-2+$\sqrt{5}$.
点评 此题考查学生掌握直线与圆相离时所满足的条件,灵活运用点到直线的距离公式化简求值,会把绝对值不等式转化为一般的二次不等式进行求解


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1或0 | B. | -1或1 | C. | 0 | D. | -1或0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c,d | B. | d,e | C. | b,e | D. | c,e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
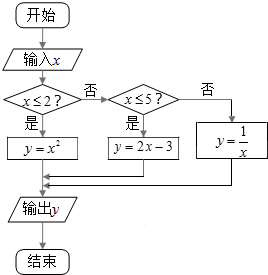 如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com