
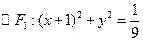 、
、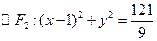 ,椭圆C的方程为
,椭圆C的方程为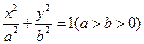 ,
,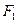 、
、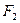 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设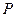 为椭圆C上一点,存在以
为椭圆C上一点,存在以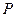 为圆心的
为圆心的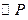 与
与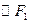 外切、与
外切、与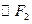 内切
内切
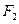 作斜率为
作斜率为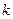 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与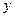 轴相交于点D,若
轴相交于点D,若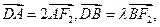 求
求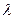 的值;
的值;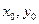 )在椭圆
)在椭圆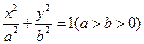 上,那么过点T
上,那么过点T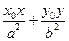 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题: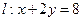 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,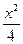 +
+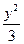 =1
=1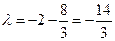
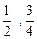 )
)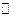 P与
P与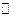
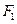 外切、
外切、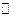
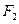 内切. 设
内切. 设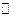 P的半径为
P的半径为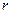 ,则
,则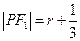
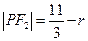 -----------------------------------2分
-----------------------------------2分
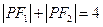 , 2
, 2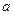 =4,2
=4,2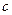 =
=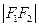 =2
=2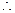
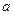 =2,c="1" , 椭圆C的方程为
=2,c="1" , 椭圆C的方程为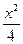 +
+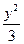 ="1 " -----------------------
="1 " ----------------------- -4分
-4分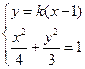
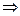
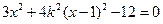
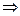
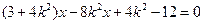 ,令A
,令A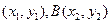 ,则
,则 ,
,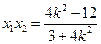 , ------------------------------------6分
, ------------------------------------6分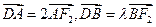
 ,
,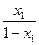 ,
, , ------------------------------------8分
, ------------------------------------8分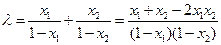
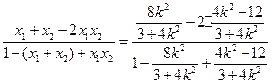
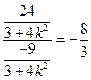 , ∴
, ∴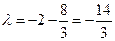 . -----------------------10分
. -----------------------10分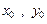 ),M(
),M(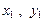 ),N(
),N(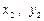 )
)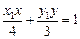

 ∴M、N在直线
∴M、N在直线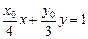 上
上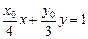 ------------------------------------12分
------------------------------------12分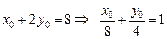
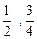 ). ------------------------------------13分
). ------------------------------------13分

 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源:不详 题型:单选题
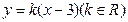 与双曲线
与双曲线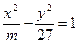 。某学生做了如下变形:由方程组
。某学生做了如下变形:由方程组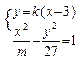 ,消去
,消去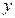 后得到形如
后得到形如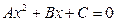 的方程。当
的方程。当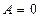 时,该方程有一解,当
时,该方程有一解,当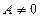 时,
时,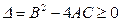 恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )
恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )A.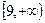 | B.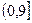 | C.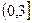 | D.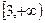 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com