
分析 实数x,y满足$\left\{{\begin{array}{l}{x-y-3≥0}\\{x+2y-6≤0}\\{x>0}\end{array}}\right.$,画出可行域,设$\frac{y}{x}$=k,则y=kx,当上述直线经过点A时,k取得最大值.
解答 解:实数x,y满足$\left\{{\begin{array}{l}{x-y-3≥0}\\{x+2y-6≤0}\\{x>0}\end{array}}\right.$,画出可行域: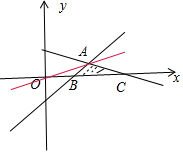
可得B(3,0),C(6,0),A(4,1).
设$\frac{y}{x}$=k,则y=kx,
当上述直线经过点A时,k取得最大值.
∴k=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了线性规划、直线方程、不等式的意义,考查了推理能力与计算能力,属于基础题.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<1} | B. | {x|2≤x<$\frac{5}{2}$} | C. | {x|2≤x≤$\frac{5}{2}$} | D. | {x|2<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 135 | B. | 105 | C. | 30 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
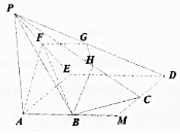 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\sqrt{2}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com