
如图,直角梯形 中,
中,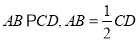 ,
,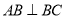 ,平面
,平面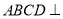 平面
平面 ,
,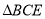 为等边三角形,
为等边三角形,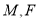 分别是
分别是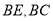 的中点,
的中点, .
.
(1)证明:
 ;
;
(2)证明: 平面
平面 ;
;
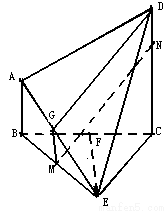
(3)若 ,求几何体
,求几何体 的体积.
的体积.

(1)由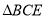 为等边三角形,
为等边三角形,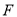 是
是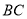 的中点知
的中点知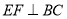 ,由平面
,由平面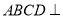 平面
平面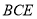 及面面垂直性质定理知,
及面面垂直性质定理知,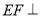 平面
平面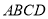 ,再由线面垂直定义得EF⊥CD;(2)取AE的中点G,连结MG,DG,因为M是BE的中点,所以MG∥且等于AB的一半,又因为AB∥CD且AB=
,再由线面垂直定义得EF⊥CD;(2)取AE的中点G,连结MG,DG,因为M是BE的中点,所以MG∥且等于AB的一半,又因为AB∥CD且AB=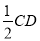 ,
,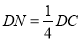 ,所以DN平行且等于MG,所以MGDN是平行四边形,所以MN∥DG,由线面平行的判定定理可得MN∥面ADE;(3)由(1)知EF⊥面ABCD,所以EF是四棱锥E-ABCD的高,由△BEC为正三角形,BC=2,可求得EF的长,由题知ABCD为直角梯形,AB⊥BC,AB=1,BC=2,所以DC=2AB=2,可求出底面ABCD的面积,所以四棱锥D-ABCD的体积就等于
,所以DN平行且等于MG,所以MGDN是平行四边形,所以MN∥DG,由线面平行的判定定理可得MN∥面ADE;(3)由(1)知EF⊥面ABCD,所以EF是四棱锥E-ABCD的高,由△BEC为正三角形,BC=2,可求得EF的长,由题知ABCD为直角梯形,AB⊥BC,AB=1,BC=2,所以DC=2AB=2,可求出底面ABCD的面积,所以四棱锥D-ABCD的体积就等于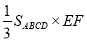 .
.
【解析】
试题分析:(1)(2)(3)
试题解析:(1)证明: 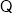
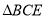 为等边三角形,
为等边三角形,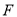 是
是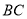 的中点
的中点

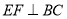 1分
1分
又因为平面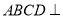 平面
平面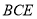 ,交线为
,交线为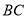 ,
, 平面
平面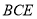
根据面面垂直的性质定理得 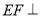 平面
平面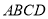 ; 3分
; 3分
又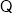
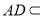 平面
平面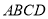

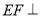
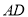 4分
4分
(2)证明:取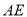 中点G,连接
中点G,连接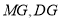
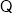
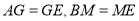

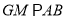 ,且
,且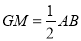 6分
6分
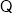
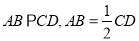 ,
,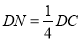

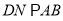 ,且
,且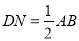 8分
8分
 四边形
四边形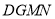 是平行四边形
是平行四边形

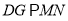 9分
9分
又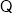
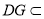 平面
平面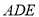 ,
, 平面
平面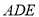

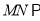 平面
平面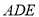 10分
10分
(3)【解析】
依题,直角梯形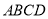 中,
中,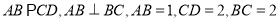
则直角梯形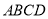 的面积为
的面积为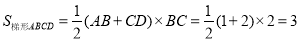 12分
12分
由(1)可知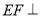 平面
平面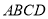 ,
,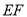 是四棱锥
是四棱锥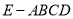 的高
的高
在等边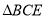 中,由边长
中,由边长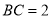 ,得
,得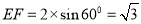 13分
13分
故几何体 的体积为
的体积为
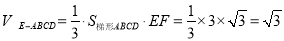 14分
14分
考点: 线面垂直定义;面面垂直性质定理;线面平行的判定;简单几何体体积计算;逻辑推理能力;运算求解能力


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源:2015届广东省等六校高三8月联考文科数学试卷(解析版) 题型:选择题
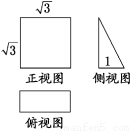
一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是( )
A.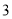 B.
B.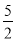 C.
C.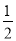 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高二下学期期中联考理科数学试卷(解析版) 题型:选择题
给出以下命题:
①对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:“夹在两个平行平面间的平行线段相等”.
② =2;
=2;
③已知函数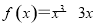 的图象与直线
的图象与直线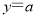 有相异三个公共点,则
有相异三个公共点,则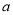 的取值范围是(-2,2)
的取值范围是(-2,2)
其中正确命题是( )
A.①②③ B.①② C.①③ D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com