
分析 (Ⅰ)设椭圆G的右焦点为F(c,0),由题意可得:b=c,且b2+c2=8,由此能求出椭圆G的方程.
(Ⅱ)以AB为底的等腰三角形ABP存在.设斜率为1的直线l的方程为y=x+m,代入$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$中,得:3x2+4mx+2m2-8=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线l的方程.
解答 解:(Ⅰ)设椭圆G的右焦点为F(c,0),
由题意可得:b=c,且b2+c2=8,∴b2=c2=4,
故a2=b2+c2=8,
∴椭圆G的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$(4分)
(Ⅱ)以AB为底的等腰三角形ABP存在.理由如下
设斜率为1的直线l的方程为y=x+m,代入$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$中,
化简得:3x2+4mx+2m2-8=0,①(6分)
因为直线l与椭圆G相交于A,B两点,
∴△=16m2-12(2m2-8)>0,
解得-2$\sqrt{3}$$<m<2\sqrt{3}$,②(8分)
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=-\frac{4m}{3}$,${x}_{1}{x}_{2}=\frac{2{m}^{2}-8}{3}$.③
于是AB的中点M(x0,y0)满足${x}_{0}=\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{2m}{3}$,${y}_{0}={x}_{0}+m=\frac{m}{3}$.
已知点P(-3,2),若以AB为底的等腰三角形ABP存在,
则kPM=-1,即$\frac{{y}_{0}-2}{{x}_{0}+3}$=-1,④,将M(-$\frac{2m}{3},\frac{m}{3}$)代入④式,
得m=3∈(-2$\sqrt{3}$,2$\sqrt{3}$)满足②(10分)
此时直线l的方程为y=x+3.(12分)
点评 本题考查椭圆方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、椭圆性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8<$\frac{f(2)}{f(1)}$<16 | B. | 4<$\frac{f(2)}{f(1)}$<8 | C. | 3<$\frac{f(2)}{f(1)}$<4 | D. | 2<$\frac{f(2)}{f(1)}$<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
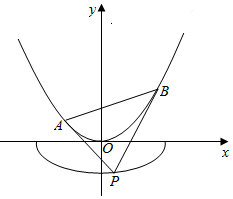 如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.
如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,f(x)>g(x) | B. | ?x1,x2∈R,f(x1)<g(x2) | ||
| C. | ?x0∈R,f(x0)=g(x0) | D. | ?x0∈R,使得?x∈R,f(x0)-g(x0)≤f(x)-g(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com