
分析 分别将两式相加减得出a与b,a与c的关系,使用作差法判断最大边,利用余弦定理解出cosC.
解答 解:∵a2-a-$\sqrt{3}$b-$\sqrt{3}$c=0,a+$\sqrt{3}$b-$\sqrt{3}$c+2=0,
两式相加得:a2-2$\sqrt{3}c$+2=0,∴c=$\frac{{a}^{2}+2}{2\sqrt{3}}$.
两式相减得:a2-2a-2$\sqrt{3}b$-2=0,∴b=$\frac{{a}^{2}-2a-2}{2\sqrt{3}}$.
显然c>b.
由b=$\frac{{a}^{2}-2a-2}{2\sqrt{3}}$>0得a2-2a-2>0,解得a>1+$\sqrt{3}$或a$<1-\sqrt{3}$(舍).
∴c-a=$\frac{{a}^{2}+2}{2\sqrt{3}}$-a=$\frac{(a-\sqrt{3})^{2}-1}{2\sqrt{3}}$>0.
∴c>a.
∴△ABC中,C为最大角.
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{a}^{2}+(\frac{{a}^{2}-2a-2}{2\sqrt{3}})^{2}-(\frac{{a}^{2}+2}{2\sqrt{3}})^{2}}{2a•\frac{{a}^{2}-2a-2}{2\sqrt{3}}}$=$\frac{\frac{-{a}^{3}+2{a}^{2}+2a}{3}}{\frac{{a}^{3}-2{a}^{2}-2a}{\sqrt{3}}}$=-$\frac{\sqrt{3}}{3}$.
故答案为:-$\frac{\sqrt{3}}{3}$.
点评 本题主要考查余弦定理的应用,不等式的解法,根据正弦定理判断最大边为c是解题的关键,考查了计算能力和转化思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 4 | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
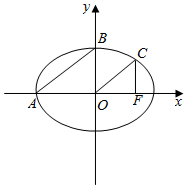 如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.
如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率是( )
如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率是( )| A. | 75% | B. | 25% | C. | 15% | D. | 40% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com