
分析 (1)将a的值代入f(x),通过讨论x的范围,求出函数的定义域即可;
(2)问题转化为a>-(|3x+2|+|1-2x|),令g(x)=|3x+2|+|1-2x|,通过讨论x的范围求出g(x)的最小值,从而求出a的范围即可.
解答 解:(1)a=-5时,f(x)=lg(|3x+2|+|1-2x|-5),
由|3x+2|+|1-2x|-5>0,
得,x≥$\frac{1}{2}$时,3x+2+2x-1-5>0,解得:x>$\frac{4}{5}$,
-$\frac{2}{3}$<x<$\frac{1}{2}$时,3x+2+1-2x-5>0,解得:x>2,(舍),
x≤-$\frac{2}{3}$时,-3x-2+1-2x-5>0,解得:x<-$\frac{6}{5}$,
综上,函数f(x)的定义域是(-∞,-$\frac{2}{3}$]∪($\frac{4}{5}$,+∞);
(2)若函数f(x)的值域为R,
只需|3x+2|+|1-2x|+a>0,
即a>-(|3x+2|+|1-2x|),
令g(x)=|3x+2|+|1-2x|,
x≥$\frac{1}{2}$时,g(x)=3x+2+2x-1=5x+1≥$\frac{7}{2}$,
-$\frac{2}{3}$<x<$\frac{1}{2}$时,g(x)=3x+2+1-2x=x+3∈($\frac{7}{3}$,$\frac{7}{2}$),
x≤-$\frac{2}{3}$时,g(x)=-3x-2+1-2x=-5x-1≥$\frac{7}{3}$,
故a≤-$\frac{7}{3}$.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及对数函数的性质,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
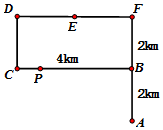 8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.
8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交且不过圆心 | D. | 相交且过圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x+1)是偶函数 | B. | f(x+1)是非奇非偶函数 | ||
| C. | f(x)=f(x+2) | D. | f(x+3)是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | ±1 | C. | 2 | D. | ±2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com