
已知函数f(x)=x2-2ax+2,当x∈[-1,+∞)时,f(x)≥a恒成立,则a的取值范围________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
设m、n是两条不同的直线,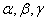 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若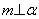 ,
,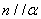 ,则
,则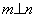 ②若
②若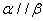 ,
,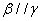 ,
,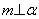 ,则
,则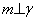
③若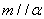 ,
,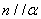 ,则
,则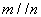 ④若
④若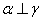 ,
, ,则
,则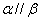
其中正确命题的序号是 ( )
(A)①和② (B)②和③ (C)③和④ (D)①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
给定两个命题,命题p:对任意实数x都有ax2>-ax-1恒成立;命题q:关于x的方程x2-x+a=0有实数根.若“p∨q”为真命题,“p∧q”为假命题,则实数a的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com