
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
分析 由已知函数解析式得到函数值域,结合存在唯一的x∈R,满足f(f(x))=2a2y2+ay,可得f(f(x))>1,即f(x)>2,进一步转化为2a2y2+ay>1,y∈(2,+∞),求解不等式得到y的范围,进一步得到a的范围得答案.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$的值域为R.
∵f(x)=2x,(x≤0)的值域为(0,1];f(x)=log2x,(x>0)的值域为R.
∴f(x)的值域为(0,1]上有两个解,
要想f(f(x))=2a2y2+ay在y∈(2,+∞)上只有唯一的x∈R满足,
必有f(f(x))>1 (2a2y2+ay>0).
∴f(x)>2,即log2x>2,解得:x>4.
当x>4时,x与f(f(x))存在一一对应的关系.
∴问题转化为2a2y2+ay>1,y∈(2,+∞),且a>0.
∴(2ay-1)(ay+1)>0,解得:y>$\frac{1}{2a}$或者y<-$\frac{1}{a}$(舍去).
∴$\frac{1}{2a}$≤2,得a$≥\frac{1}{4}$.
故选:C.
点评 本题考查函数的最值及其几何意义,考查数学转化思想方法,考查逻辑思维能力与推理运算能力,难度较大.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
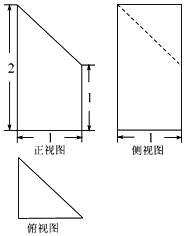
| A. | ${\frac{5}{6}_{\;}}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $64-\frac{32π}{3}$ | B. | 64-16π | C. | $64-\frac{16π}{3}$ | D. | $64-\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
| 频数 | 5 | 9 | 11 | 9 | 7 | 9 |
| 满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com