练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知命题方程表示焦点在轴上的椭圆，命题双曲线的离心率，若“”为假命题，“”为真命题，则的取值范围是__________．

    【答案】

    【解析】分析：根据椭圆的性质，可求出命题方程表示焦点在轴上的椭圆为真命题时，实数的取值范围；根据双曲线的性质，可得命题双曲线的离心率为真命题时，实数的取值范围；进而结合“”为假命题，“”为真命题即命题中有且只有一个为真命题，得到答案．

    详解：若命题方程表示焦点在轴上的椭圆为真命题时；
    则
    解得 ，
    则命题为假命题时，或，
    若命题双曲线的离心率为真命题时；
    则 即即

    则命题为假命题时，，或 ，
    ∵“”为假命题，“”为真命题，一次命题中有且只有一个为真命题，
    当真假时，0，
    当假真时，，
    综上所述，实数的取值范围是：，或．
    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某种农作物可以生长在滩涂和盐碱地，它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度对亩产量(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表：

    海水浓度

    亩产量（吨）

    残差

    绘制散点图发现,可以用线性回归模型拟合亩产量(吨)与海水浓度之间的相关关系，用最小二乘法计算得与之间的线性回归方程为.

    （1）求的值；

    （2）统计学中常用相关指数来刻画回归效果，越大，回归效果越好，如假设，就说明预报变量的差异有是解释变量引起的.请计算相关指数(精确到),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的？

    （附：残差，相关指数，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着共享单车的蓬勃发展，越来越多的人将共享单车作为短距离出行的交通工具.为了解不同年龄的人们骑乘单车的情况，某共享单车公司对某区域不同年龄的骑乘者进行了调查，得到数据如下：

    年龄

    15

    25

    35

    45

    55

    65

    骑乘人数

    95

    80

    65

    40

    35

    15

    （1）求关于的线性回归方程，并估计年龄为40岁人群的骑乘人数；

    （2）为了回馈广大骑乘者，该公司在五一当天通过向每位骑乘者的前两次骑乘分别随机派送一张面额为1元，或2元，或3元的骑行券.已知骑行一次获得1元券，2元券，3元券的概率分别是，，，且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车，记该骑乘者当天获得的骑行券面额之和为，求的分布列和数学期望.

    参考公式： ，.

    参考数据：，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知球为正四面体的外接球，，过点作球的截面，则截面面积的取值范围为____________________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛，下面是他们的一段对话．甲说：“乙参加‘演讲’比赛”；乙说：“丙参加‘诗词’比赛”；丙说“丁参加‘演讲’比赛”；丁说：“戊参加‘诗词’比赛”；戊说：“丁参加‘诗词’比赛”．

    已知这5个人中有2人参加“演讲”比赛，有3人参加“诗词”比赛，其中有2人说的不正确，且参加“演讲”的2人中只有1人说的不正确．根据以上信息，可以确定参加“演讲”比赛的学生是

    A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方形内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知无穷数列，是公差分别为、的等差数列，记（），其中表示不超过的最大整数，即.

    （1）直接写出数列，的前4项，使得数列的前4项为：2，3，4，5；

    （2）若，求数列的前项的和；

    （3）求证：数列为等差数列的必要非充分条件是.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某生产企业研发了一种新产品，该产品在试销一个阶段后得到销售单价（单位：元）和销售量（单位：万件）之间的一组数据，如下表所示：

    销售单价/元

    销售量/万件

    （1）根据表中数据，建立关于的线性回归方程；

    （2）从反馈的信息来看，消费者对该产品的心理价（单位：元/件）在内，已知该产品的成本是元，那么在消费者对该产品的心理价的范围内，销售单价定为多少时，企业才能获得最大利润？（注：利润=销售收入-成本）

    参考数据：

    参考公式：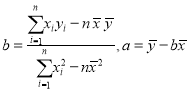

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，，动点满足，记M的轨迹为曲线C．

    （1）求曲线C的方程；

    （2）过坐标原点O的直线l交C于P、Q两点，点P在第一象限，轴，垂足为H．连结QH并延长交C于点R．

    （i）设O到直线QH的距离为d．求d的取值范围;

    （ii）求面积的最大值及此时直线l的方程．

    查看答案和解析>>

    同步练习册答案