
【题目】已知点![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,记M的轨迹为曲线C.
,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过坐标原点O的直线l交C于P、Q两点,点P在第一象限,![]() 轴,垂足为H.连结QH并延长交C于点R.
轴,垂足为H.连结QH并延长交C于点R.
(i)设O到直线QH的距离为d.求d的取值范围;
(ii)求![]() 面积的最大值及此时直线l的方程.
面积的最大值及此时直线l的方程.
【答案】(1) ![]() ;(2) (i)
;(2) (i)![]() (ii)面积最大值为
(ii)面积最大值为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
【解析】
(1)根据题意列出方程求解即可
(2)联立直线与圆的方程,得出P、Q、H三点坐标,表示出QH直线方程,采用点到直线距离公式求解;利用圆的几何关系,表示出三角形的底和高,再结合函数最值问题进行求解
(1)由![]() 及两点距离公式,
及两点距离公式,
有![]() ,
,
化简整理得,![]() .
.
所以曲线C的方程为![]() ;
;
(2)(i)设直线l的方程为![]() ;
;
将直线l的方程与圆C的方程联立,消去y,
得(![]() ,解得
,解得![]()
因此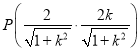 ,
,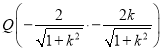 ,
,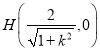 ,
,
所以直线QH的方程为 .
.
![]() 到直线QH的距离
到直线QH的距离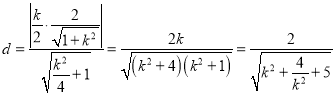 ,
,
当![]() 时.
时.![]() ,所以,
,所以,![]()
(ii)过O作![]() 于D,则D为QR中点,且由(i)知
于D,则D为QR中点,且由(i)知![]() ,
,
![]() ,
,![]() ,
,
又由![]() ,故
,故![]() 的面积
的面积![]() ,
,
由![]() ,有
,有![]() ,所以
,所以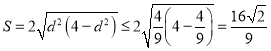 ,
,
当且仅当![]() 时,等号成立,且此时由(i)有
时,等号成立,且此时由(i)有![]() ,即
,即![]() .
.
综上,![]() 的面积最大值为的面积最大值为
的面积最大值为的面积最大值为![]() ,且当面积最大时直线
,且当面积最大时直线![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须整改.若整改后经复查仍不合格,则强制关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率是0.8.计算(结果精确到0.01):
(1)恰好有两家煤矿必须整改的概率.
(2)平均有多少家煤矿必须整改?
(3)至少关闭一家煤矿的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,定义域为![]() 上的函数
上的函数![]() 是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.
是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.

(1)求![]() 的解析式;
的解析式;
(2)若![]() 关于的方程
关于的方程![]() 有三个不同解,求
有三个不同解,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y![]() ,有
,有![]() ,f(1)=2,且
,f(1)=2,且![]() .
.
(1)求f(0)的值;
(2)求证:对任意x![]() ,都有f(x)>0;
,都有f(x)>0;
(3)解不等式f(3![]() 2x)>4.
2x)>4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ln(x+1)+ ![]() +ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=
+ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y= ![]() x在(0,0)点相切.
x在(0,0)点相切.
(1)求a,b的值;
(2)证明:当0<x<2时,f(x)< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com