练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．若$α∈（2kπ+\frac{π}{4}，2kπ+\frac{π}{2}）$（k∈Z），则sinα，cosα，tanα的大小关系为（　　）
    A．tanα＞sinα＞cosαB．tanα＞cosα＞sinαC．tanα＜sinα＜cosαD．tanα＜cosα＜sinα

    分析 利用单位圆中的正切线、正弦线、余弦线，即可得出结论．

    解答 解：∵$α∈（2kπ+\frac{π}{4}，2kπ+\frac{π}{2}）$（k∈Z），
    所以在单位圆中，做出角α的正切线、正弦线、余弦线，

    可得正切线最长，余弦线最短，
    所以有tanα＞sinα＞cosα，
    故选：A

    点评 本题考查利用单位圆中的正切线、正弦线、余弦线的大小来比较对应的三角函数的大小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

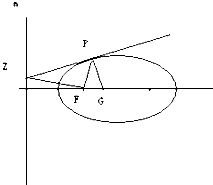    13．已知：如图，设P为椭圆上的任意一点，过点P作椭圆的切线，交准线m于点Z，此时FZ⊥FP，过点P作PZ的垂线交椭圆的长轴于点G，椭圆的离心率为e，求证：FG=e•FP．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图，已知PA是⊙O的切线，A是切点，直线PO交⊙O于B、C两点，D是OC的中点，连结AD并延长交⊙O于点E，若PA=2$\sqrt{3}$，∠APB=30°．
    （1）求∠ABO的大小；
    （2）求AD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若$cos（\frac{π}{6}-α）=m，（|m|≤1）$，则$sin（\frac{2π}{3}-α）$的值为（　　）
    A．-mB．$-\frac{m}{2}$C．$\frac{m}{2}$D．m

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=x2-（a+1）x+a，g（x）=-（a+4）x-4+a，a∈R
    （1）x∈R，比较f（x）与g（x）的大小；
    （2）当x∈（0，+∞）时，解不等式f（x）＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．某饮料销售点销售某品牌饮料，饮料的零售价x（元/瓶）与销量y（瓶）的关系统计如下：
    零售价x（元/瓶）3.03.23.43.63.84.0
    销量y（瓶）504443403528
    由表中数据得线性回归方程：$\widehat{y}$=-20x+a，当零售价为每瓶3.7元时，估计该销售点销售的这种饮料的瓶数为（　　）
    A．39B．38C．37D．36

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．若正三角形内切圆的半径为r，则该正三角形的周长C（r）=6$\sqrt{3}$r，面积S（r）=3$\sqrt{3}$r2，发现S′（r）=C（r）．相应地，若正四面体内切球的半径为r，则该正四面体的表面积S（r）=24$\sqrt{3}$r2．请用类比推理的方法猜测该正四面体的体积V（r）=8$\sqrt{3}$r3（写出关于r的表达式）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．极坐标方程ρcosθ=2sin2θ表示的曲线为（　　）
    A．一条射线和一个圆B．一条直线和一个圆
    C．两条直线D．一个圆

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知sinα=$\frac{1}{3}$，则cos（α+$\frac{3π}{2}$）=（　　）
    A．$\frac{2\sqrt{2}}{3}$B．-$\frac{2\sqrt{2}}{3}$C．$\frac{1}{3}$D．-$\frac{1}{3}$

    查看答案和解析>>

    同步练习册答案