
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
| A. | 39 | B. | 38 | C. | 37 | D. | 36 |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
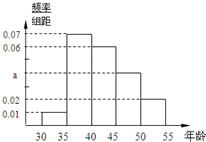 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tanα>sinα>cosα | B. | tanα>cosα>sinα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由a(b+c)=ab+ac类比得到loga(x+y)=logax+logby | |
| B. | 由a(b+c)=ab+ac类比得到cos(x+y)=cosx+cosy | |
| C. | 由(a+b)c=ac+bc类比$\frac{a+b}{c}$=$\frac{a}{c}$+$\frac{b}{c}$(c≠0) | |
| D. | 由(ab)n=anbn类比得到(x+y)n=xn+yn |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m、n与α所成的角相等,则m∥n | B. | 若n∥α,m∥β,α∥β,则m∥n | ||
| C. | 若n?α,m?β,m∥n,则α∥β | D. | 若n⊥α,m⊥β,α⊥β,则n⊥m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com