练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在数列{an}中，a1＝2i(i为虚数单位)，(1＋i)an＋1＝(1－i)an(n∈N*)，则a2 012的值为(　　)

    A．－2                            B．0

    C．2                              D．2i


    A　∵(1＋i)an＋1＝(1－i)an，

    ∴＝－i，故{an}是以2i为首项，－i为公比的等比数列，∴a2 012＝2i×(－i)2 012－1＝2i×(－i)4×502＋3＝2i×i＝－2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若两条曲线的极坐标方程分别为ρ＝1与ρ＝2cos，它们相交于A、B两点，求线段AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，PA切圆O于点A，割线PBC交圆O于点B、C，∠APC的角平分线分别与AB、AC相交于点D、E，求证：

    (1) AD＝AE；

    (2) AD2＝DB·EC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|x－a|.

    (1) 若不等式f(x)≤3的解集为{x|－1≤x≤5}，求实数a的值；

    (2) 在(1)的条件下，若f(x)＋f(x＋5)≥m对一切实数x恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     解不等式：|x－1|>.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列推理中属于归纳推理且结论正确的是(　　)

    A．设数列{an}的前n项和为Sn.由an＝2n－1，求出S1＝12，S2＝22，S3＝32，…，推断：Sn＝n2

    B．由f(x)＝xcos x满足f(－x)＝－f(x)对∀x∈R都成立，推断：f(x)＝xcos x为奇函数

    C．由圆x2＋y2＝r2的面积S＝πr2，推断：椭圆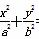＝1(a＞b＞0)的面积S＝πab

    D．由(1＋1)2＞21，(2＋1)2＞22，(3＋1)2＞23，…，推断：对一切n∈N*，(n＋1)2＞2n

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二维空间中圆的一维测度(周长)l＝2πr，二维测度(面积)S＝πr2，观察发现S′＝l；三维空间中球的二维测度(表面积)S＝4πr2，三维测度(体积)V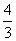＝πr3，观察发现V′＝S.则由四维空间中“超球”的三维测度V＝8πr3，猜想其四维测度W＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数y＝f(x)的图象关于y轴对称，且当x∈(－∞，0)时，f(x)＋xf′(x)＜0成立，a＝(20.2)·f(20.2)，b＝(logπ3)·f(logπ3)，c＝(log39)·f(log39)，则a，b，c的大小关系是(　　)

    A．b＞a＞c                        B．c＞a＞b

    C．c＞b＞a                        D．a＞c＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝若函数y＝f(x)－2有3个零点，则实数a的值为(　　)

    A．－4                          B．－2

    C．0                            D．2

    查看答案和解析>>

    同步练习册答案