
分析 由题意知X的可能取值为2,3,4,5,分别求出相应在的概率,由此能求出X的分布列和数学期望.
解答 解:由题意知X的可能取值为2,3,4,5,
P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{10}$,
P(X=3)=$\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{5}^{2}}•\frac{1}{3}$=$\frac{1}{5}$,
P(X=4)=$\frac{{C}_{2}^{1}{C}_{3}^{2}}{{C}_{5}^{3}}•\frac{1}{2}$=$\frac{3}{10}$,
P(X=5)=$\frac{{C}_{2}^{1}{C}_{3}^{3}}{{C}_{5}^{4}}•\frac{1}{1}$=$\frac{2}{5}$.
∴X的分布列为:
| X | 2 | 3 | 4 | 5 |
| P | $\frac{1}{10}$ | $\frac{1}{5}$ | $\frac{3}{10}$ | $\frac{2}{5}$ |
点评 本题考查离散型随机变量的分布列、数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=g(x)是奇函数 | B. | y=g(x)的图象关于点(-$\frac{π}{2}$,0)对称 | ||
| C. | y=g(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=g(x)的周期为π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
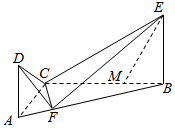 如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF.D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.
如图,直角三角形ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF.D,E是平面ABC同一侧的两点,AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{12}{25}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com