Question

10．某高中学校为了解中学生的身高情况，从该校同年龄段的所有学生中随机抽取50名学生测量身高，由测量得到频率分布表和频率分布直方图（部分）如下：

身高	[145，155）	[155，165）	[165，175）	[175，185）	[185，195]
频数	3	m	19	n	4

（1）求m，n并在该题答题纸区域内补全频率分布直方图；
（2）请用这50名学生的身高数据来估计该校这个年龄段的学生身高平均数是多少？（同一组中的数据用该组的中点值作代表）；
（3）从[145，155）和[185，195]这两组中任意取出两名学生，求这两名学生身高差距超过10cm的概率．

Answer 1

分析 （1）由频率分布直方图得身高在[155，165）内的频率为0.26，从而能求出m，进而能求出n，由此能求出身高在[155，165）内的小矩形的高，从而补全频率分布直方图．
（2）利用频率分布直方图能用这50名学生的身高数据来估计该校这个年龄段的学生身高平均数．
（3）求出身高在[145，155）内的学生有3人，身高在[185，195]内的学生有4人，从这两组中任意取出两名学生，基本事件总数n=${C}_{7}^{2}$=21，这两名学生身高差距超过10cm包含的基本事件个数m=${C}_{3}^{1}{C}_{4}^{1}=12$，由此能求出这两名学生身高差距超过10cm的概率．

解答 解：（1）由频率分布直方图得身高在[155，165）内的频率为0.026×10=0.26，
∴m=0.26×50=13，
∴n=50-3-13-19-4=11，
∴身高在[155，165）内的频率为：$\frac{11}{50}$=0.22，
∴频率分布直方图中身高在[155，165）内的小矩形的高为：$\frac{0.22}{10}$=0.022，
补全频率分布直方图如下图：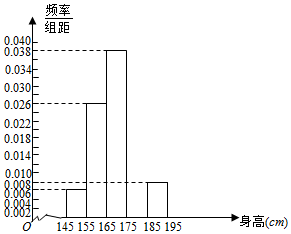

（2）用这50名学生的身高数据来估计该校这个年龄段的学生身高平均数为：
0.006×10×150+0.026×10×160+0.038×10×170+0.022×10×180+0.008×10×190=170．
（3）身高在[145，155）内的学生有0.006×10×50=3人，
身高在[185，195]内的学生有0.008×10×50=4人，
从这两组中任意取出两名学生，基本事件总数n=${C}_{7}^{2}$=21，
这两名学生身高差距超过10cm包含的基本事件个数m=${C}_{3}^{1}{C}_{4}^{1}=12$，
∴这两名学生身高差距超过10cm的概率p=$\frac{m}{n}=\frac{12}{21}$=$\frac{4}{7}$．

点评 本题考查频率分布直方图的应用，考查概率的求法，是基础题，解题时要认真审题，注意频率分布直方图的应用，考查古典概型的合理运用．