
【题目】函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(1)+f(2)+f(3)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( ) 
A.f(x)= ![]() sin
sin ![]() x+1,S=2016
x+1,S=2016
B.f(x)= ![]() cos
cos ![]() x+1,S=2016
x+1,S=2016
C.f(x)= ![]() sin
sin ![]() x+1,S=2016.5
x+1,S=2016.5
D.f(x)= ![]() cos
cos ![]() x+1,S=2016.5
x+1,S=2016.5
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】在y=2x2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,则点P的坐标是( )
A.(﹣2,1)
B.(1,2)
C.(2,1)
D.(﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量,有下列四个命题:
①若 ![]() .
.
② ![]() =(1,1),
=(1,1), ![]() =(2,x),若
=(2,x),若 ![]() 与
与 ![]() 平行,则x=2.
平行,则x=2.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,则
|,则 ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量 ![]() 同方向的单位向量为(
同方向的单位向量为( ![]() ).
).
其中真命题的序号为 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分 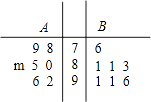
(1)求m的值,并计算A班7名学生成绩的方差s2;
(2)从成绩在90分以上的学生中随机抽取两名学生,求至少有一名A班学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1 . 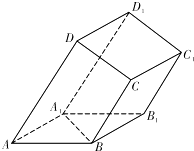
(Ⅰ)求证:A1B⊥BC;
(Ⅱ)若AD=AB=3BC,∠A1AB=60°,点D在平面ABB1A1上的射影恰为线段A1B的中点,求平面DCC1D1与平面ABB1A1所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,求x的值.
,求x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某河道中过度滋长一种藻类,环保部门决定投入生物净化剂净化水体. 因技术原因,第t分钟内投放净化剂的路径长度![]() (单位:m),净化剂净化水体的宽度
(单位:m),净化剂净化水体的宽度![]() (单位:m)是时间t(单位:分钟)的函数:
(单位:m)是时间t(单位:分钟)的函数: ![]() (
(![]() 由单位时间投放的净化剂数量确定,设
由单位时间投放的净化剂数量确定,设![]() 为常数,且
为常数,且![]() ).
).
(1)试写出投放净化剂的第t分钟内净化水体面积![]() 的表达式;
的表达式;
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com