
【题目】已知函数f(x)= ![]() sin2ωxcosφ+cos2ωxsinφ+
sin2ωxcosφ+cos2ωxsinφ+ ![]() cos(
cos( ![]() +φ)(0<φ<π),其图象上相邻两条对称轴之间的距离为π,且过点(
+φ)(0<φ<π),其图象上相邻两条对称轴之间的距离为π,且过点( ![]() ). (I)求ω和φ的值;
). (I)求ω和φ的值;
(II)求函数y=f(2x),x∈[0, ![]() ]的值域.
]的值域.
【答案】解:f(x)= ![]() sin2ωxcosφ+cos2ωxsinφ+
sin2ωxcosφ+cos2ωxsinφ+ ![]() cos(
cos( ![]() +φ)(0<φ<π), f(x)=
+φ)(0<φ<π), f(x)= ![]() sin2ωxcosφ+cos2ωxsinφ﹣
sin2ωxcosφ+cos2ωxsinφ﹣ ![]() sinφ
sinφ
f(x)= ![]() sin2ωxcosφ+sinφ(cos2ωx﹣
sin2ωxcosφ+sinφ(cos2ωx﹣ ![]() )
)
f(x)= ![]() sin2ωxcosφ+
sin2ωxcosφ+ ![]() cos2ωxsinφ
cos2ωxsinφ
f(x)= ![]() sin(2ωx+φ),
sin(2ωx+φ),
(I)∵图象上相邻两条对称轴之间的距离为π,∴T=2π,
又∵T= ![]() ,∴ω=
,∴ω= ![]() ,
,
图象过点( ![]() ),∴
),∴ ![]() =
= ![]() sin(±1×
sin(±1× ![]() +φ),
+φ),
解得: ![]() ,
,
∴f(x)= ![]() sin(x+
sin(x+ ![]() )或f(x)=
)或f(x)= ![]() sin(﹣x+
sin(﹣x+ ![]() );
);
(Ⅱ)∵y=f(2x),
又∵x∈[0, ![]() ],
],
∴2x+ ![]() ∈[
∈[ ![]() ],
],
结合正弦函数的图象和性质:当 ![]() 时,y取得最大值,即
时,y取得最大值,即 ![]() ,
,
当 ![]() 时,y取得最小值,即
时,y取得最小值,即 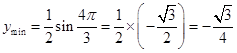 ,
,
所以函数y=f(2x),x∈[0, ![]() ]的值域为
]的值域为 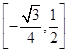 .
.
【解析】(I)将函数进行化简,结合三角函数的图象和性质和已知坐标,即可求函数ω和φ的值;(II)求出函数y=f(2x)的解析式,根据x∈[0, ![]() ]求出函数y=f(2x)的范围,在求其范围内的最大值和最小值,即可得到值域. ∴y=f(2x)=
]求出函数y=f(2x)的范围,在求其范围内的最大值和最小值,即可得到值域. ∴y=f(2x)= ![]() sin(2x+
sin(2x+ ![]() ),【注意:只需要一个解析式即可,其实两个解析式化简是一样的】
),【注意:只需要一个解析式即可,其实两个解析式化简是一样的】
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】若f(x)=Asin(ωx+)(其中A>0,|φ| ![]() )的图象如图,为了得到
)的图象如图,为了得到 ![]() 的图象,则需将f(x)的图象( )
的图象,则需将f(x)的图象( ) 
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(﹣1,0),离心率e= ![]() .
. 
(1)求椭圆G 的标准方程;
(2)已知直线l1:y=kx+m1与椭圆G交于 A,B两点,直线l2:y=kx+m2(m1≠m2)与椭圆G交于C,D两点,且|AB|=|CD|,如图所示. ①证明:m1+m2=0;
②求四边形ABCD 的面积S 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c有两个极值点x1 , x2 , 若x2<f(x1)<x1 , 则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数可能为( )
A.3,4,5
B.4,5,6
C.2,4,5
D.2,3,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x+3|.
(1)解不等式f(x)≥8;
(2)若不等式f(x)<a2﹣3a的解集不是空集,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M. 
(1)求证:DC是⊙O的切线;
(2)求证:AMMB=DFDA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如右表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5~7分钟,乙每次解答一道几何题所用的时间在6~8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为 X,求 X的分布列及数学期望 EX. 附表及公式
P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)f(y)=f(x+y),若a1= ![]() ,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
A.[ ![]() ,2)
,2)
B.[ ![]() ,2]
,2]
C.[ ![]() ,1)
,1)
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数).
为常数).
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)若不等式![]() 在
在![]() 时有解,求实数
时有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,是否存在正数
,是否存在正数![]() ,使得对于区间
,使得对于区间![]() 上的任意三个实数
上的任意三个实数![]() ,
,![]() ,
,![]() ,都存在以
,都存在以![]() ,
,![]() ,
,![]() 为边长的三角形?若存在,试求出这样的
为边长的三角形?若存在,试求出这样的![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com