
分析 (1)先假设存在,列出方程,根据方程无解,得出不存在;
(2)化简函数式为h(x)=1-x+$\frac{{{x^2}-x+1}}{x-1}$=$\frac{1}{x-1}$+1,从而判断函数图象关于点(1,1)中心对称;
(3)运用双勾函数的图象和性质,并通过分类讨论确定函数的最值.
解答 解:(1)根据生成函数的定义,设存在a,b使得h(x)=a•f1(x)+b•f2(x),
则x2-x+1=a(x2-x)+b(x2+x+1)=(a+b)x2+(b-a)x+b,
对比两边的系数可知,$\left\{\begin{array}{l}{a+b=1}\\{b-a=-1}\\{b=1}\end{array}\right.$,方程无解,
所以,h(x)不是f1(x),f2(x)的生成函数;
(2)因为a=b=1,所以,h(x)=1-x+$\frac{{{x^2}-x+1}}{x-1}$,
而h(x)=1-x+$\frac{{{x^2}-x+1}}{x-1}$=(1-x)+$\frac{x^2-x}{x-1}$+$\frac{1}{x-1}$=$\frac{1}{x-1}$+1,
该函数的图象为双曲线,对称中心为(1,1);
(3)根据题意,h(x)=2x+$\frac{b}{x-1}$=2(x-1)+$\frac{b}{x-1}$+2(x≥2),
根据基本不等式,2(x-1)+$\frac{b}{x-1}$≥2$\sqrt{2b}$,
当且仅当:x=$\sqrt{\frac{b}{2}}$+1时,取“=”,
因此,函数h(x)单调性为,x∈(1,$\sqrt{\frac{b}{2}}$+1)上单调递减,x∈($\sqrt{\frac{b}{2}}$+1,+∞)上单调递增,
故令$\sqrt{\frac{b}{2}}$+1=2,解得b=2,最值情况分类讨论如下:
①当b∈(0,2]时,$\sqrt{\frac{b}{2}}$+1≤2,
所以,当x≥2时,h(x)单调递增,h(x)min=h(2)=b+4=5,解得b=1,符合题意;
②当b∈(2,+∞)时,$\sqrt{\frac{b}{2}}$+1>2,
所以,当x≥2时,h(x)先减后增,h(x)min=h($\sqrt{\frac{b}{2}}$+1)=2$\sqrt{2b}$+2=5,解得b=$\frac{9}{8}$,不合题意;
综合以上讨论得,实数b的值为1.
点评 本题主要考查了函数解析式的求法,函数图象对称中心的确定,以及运用函数的单调性确定函数的最值,属于难题.


科目:高中数学 来源: 题型:选择题
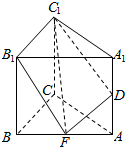 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<k<4 | B. | k>4 | C. | k<0 | D. | k<1或k>4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥$\frac{5}{4}$ | B. | k>-$\frac{5}{4}$ | C. | k≤-$\frac{5}{4}$ | D. | k<-$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com