
分析 (1)求出函数的对数,计算f′(2)=0,求出a的值,从而求出h(x)的表达式,求出切线方程即可;
(2)问题等价于对任意的x1,x2∈[1,e]都有[f(x)]min≥[g(x)]max,通过讨论a的范围,求出函数的单调性,从而求出f(x)的最小值和g(x)的最大值,确定a的范围即可.
解答 解:(1)∵$f'(x)=1-\frac{a^2}{x^2}$,x=2是函数f(x)的极值点,
∴f'(2)=0,即$1-\frac{a^2}{4}$,又a≥1,∴a=2,
∴$h(x)=f(x)+g(x)=2x+\frac{4}{x}+lnx$,
∴$h'(x)=2-\frac{4}{x^2}+\frac{1}{x}$,
∴$k=h'(1)=2-\frac{4}{1^2}+\frac{1}{1}=-1$,又h(1)=6,
∴所求的切线方程是 y-1=-(x-6),
即 y=-x+7.
(2)对任意的x1,x2∈[1,e]都有f(x1)≥g(x2)成立,
等价于对任意的x1,x2∈[1,e]都有[f(x)]min≥[g(x)]max,
当x∈[1,e]时,$g'(x)=1+\frac{1}{x}>0$,
∴函数g(x)=x+lnx在[1,e]上是增函数,
∴[g(x)]max=g(e)=e+1,
∵$f'(x)=1-\frac{a^2}{x^2}=\frac{{({x+a})({x-a})}}{x^2}$,且x∈[1,e],a>0;
①当1≤a≤e时,
若1≤x<a,则$f'(x)=\frac{{({x+a})({x-a})}}{x^2}<0$,
若a<x≤e,则$f'(x)=\frac{{({x+a})({x-a})}}{x^2}>0$,
∴函数$f(x)=x+\frac{a^2}{x}$在[1,a)上是减函数,在(a,e]上是增函数,
∴[f(x)]min=f(a)=2a,
由2a≥e+1,得a≥$\frac{e+1}{2}$,又1≤a≤e,∴$\frac{e+1}{2}$≤a≤e;
②.当a>e且x∈[1,e]时,$f'(x)=\frac{{({x+a})({x-a})}}{x^2}<0$,
∴函数$f(x)=x+\frac{a^2}{x}$在[1,e]上是减函数,
∴${[{f(x)}]_{min}}=f(e)=e+\frac{a^2}{e}$,
由$e+\frac{a^2}{e}$≥e+1,得a≥$\sqrt{e}$,
又a>e,∴a>e,
综上所述,a的取值范围为$[{\frac{e+1}{2},+∞})$.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
| 每小时生产有缺点的零件数y(件) | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
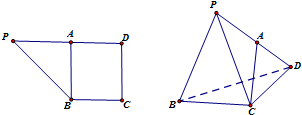 如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.
如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{1+x-(2n+1){x^n}+(2n-1){x^{n+1}}}}{{{{(1-x)}^2}}}$ | B. | $\frac{{1+x-(2n+1){x^n}+(2n-1){x^{n+1}}}}{1-x}$ | ||
| C. | $\frac{{1+x-(2n+1){x^n}+(2n-3){x^{n+1}}}}{{{{(1-x)}^2}}}$ | D. | $\frac{{1+x-(2n-1){x^n}+(2n+1){x^{n+1}}}}{{{{(1-x)}^2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
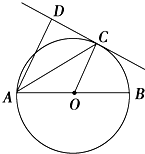 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com