练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．计算：8${\;}^{\frac{2}{3}}$×16${\;}^{-\frac{1}{2}}$+10lg3+lg$\sqrt{\frac{3}{5}}$+$\frac{1}{2}$lg$\frac{5}{3}$．

    分析 利用指数幂与对数的运算性质即可得出．

    解答 解：原式=22×${2}^{4×（-\frac{1}{2}）}$+3+$lg\sqrt{\frac{3}{5}}×\sqrt{\frac{5}{3}}$
    =4×$\frac{1}{4}$+3+lg1
    =4．

    点评 本题考查了指数幂与对数的运算性质，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点（1，$\frac{3}{2}$），左右焦点为F1、F2，右顶点为A，上顶点为B，且|AB|=$\frac{{\sqrt{7}}}{2}$|F1F2|．
    （1）求椭圆E的方程；
    （2）直线l：y=-x+m与椭圆E交于C、D两点，与以F1、F2为直径的圆交于M、N两点，且$\frac{{\sqrt{7}|CD|}}{|MN|}$=$\frac{36}{7}$，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

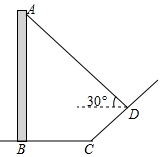    4．如图，直立于地面上的电线杆AB，在阳光下落在水平地面和坡面上的影子分别是BC，CD，测得BC=6米，CD=4米，∠BCD=150°，在D处测得电线杆顶端A的仰角为30°，试求电线杆的高度（结果保留根号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

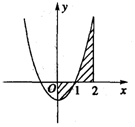    1．由曲线y=x 2-1，直线x=0，x=2和x轴围成的封闭图形的面积（如图）可表示为（　　）
    A．${∫}_{0}^{2}$（x 2-1）dxB．${∫}_{0}^{2}$|（x 2-1）|dx
    C．|${∫}_{0}^{2}$（x 2-1）dx|D．${∫}_{0}^{1}$（x 2-1）dx+${∫}_{1}^{2}$（x 2-1）dx

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在平面直角坐标系xOy中，圆C的参数方程为$\left\{\begin{array}{l}{x=-5+\sqrt{2}cost}\\{y=3+\sqrt{2}sint}\end{array}\right.$（t为参数），在以原点O为极点，x轴的非负半轴为极轴建立的极坐标系中，直线l的极坐标方程为$\frac{\sqrt{2}}{2}$ρcos（θ+$\frac{π}{4}$）=-1．
    （1）求圆C的普通方程和直线l的直角坐标方程；
    （2）设直线l与x轴，y轴分别交于A，B两点，点P是圆C上任一点，求A，B两点的极坐标和△PAB面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在△ABC中，A=$\frac{π}{6}，BC=\frac{{4\sqrt{3}}}{3}$，AB=4，则C=（　　）
    A．$\frac{π}{6}$B．$\frac{2π}{3}$C．$\frac{π}{3}$或$\frac{2π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．f（x）是定义在R上图形关于y轴对称，且在[0，+∞）上是减函数，下列不等式一定成立的是（　　）
    A．f[${\frac{2}{{2-{a^2}}}}$]＜f（${{a^2}-2a+\frac{5}{4}}$）B．f[-cos60°]＜f（tan30°）
    C．f[-（cos60°）2]≥f（${{a^2}-2a+\frac{5}{4}}$）D．f[-sin45°]＞f（-3a+2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知Rt△ABC的顶点分别为A（1，2），B（-1，-2）．，C（1，-2），圆E是△ABC的外接圆．
    （I）求圆E的方程；
    （II）求直线lmx-y-m+1=0被圆E截得的最短弦长及对应的直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．设△ABC的三个内角A、B、C的对边分别为a、b、c，且asinAsinB+bcos2A=$\sqrt{2}$a，则角A的取值范围为（0，$\frac{π}{4}$]．

    查看答案和解析>>

    同步练习册答案