
分析 (1)由圆C的参数方程消去t得到圆C的普通方程,由直线l的极坐标方程,利用两角和与差的余弦函数公式化简,根据x=ρcosθ,y=ρsinθ转化为直角坐标方程即可;
(2)直线l与x轴,y轴的交点为A(0,2),B(-2,0),化为极坐标,并求出|AB|的长,根据P在圆C上,设出P坐标,利用点到直线的距离公式表示出P到直线l的距离,利用余弦函数的值域确定出最小值,即可确定出三角形PAB面积的最小值.
解答 解:(1)由$\left\{\begin{array}{l}{x=-5+\sqrt{2}cost}\\{y=3+\sqrt{2}sint}\end{array}\right.$(t为参数),消去参数t,得圆C的普通方程(x+5)2+(y-3)2=2.
由$\frac{\sqrt{2}}{2}$ρcos(θ+$\frac{π}{4}$)=-1,得ρcosθ-ρsinθ=-2,
所以直线l的直角坐标方程为x-y+2=0.
(2)直线l与x轴,y轴的交点为A(0,2),B(-2,0),化为极坐标为A(2,π),B(2,$\frac{π}{2}$),
设P点的坐标为(-5+$\sqrt{2}$cost,3+$\sqrt{2}$sint),
∴P点到直线l的距离为d=$\frac{|-5+\sqrt{2}cost-3-\sqrt{2}sint+2|}{\sqrt{2}}$=$\frac{|-6+2cos(t+\frac{π}{4})|}{\sqrt{2}}$
∴dmin=2$\sqrt{2}$,
∵|AB|=2$\sqrt{2}$,
则△PAB面积的最小值是S=$\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$=4.
点评 此题考查了圆的参数方程,以及简单曲线的极坐标方程,熟练掌握参数方程与普通方程间的转换是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
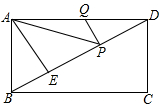 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P,Q分别在BD,AD上,| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$,$\overrightarrow{b}$方向相同 | |
| B. | $\overrightarrow{a}$,$\overrightarrow{b}$两向量中至少有一个为零向量 | |
| C. | ?λ∈R,$\overrightarrow{b}$=λ$\overrightarrow{a}$ | |
| D. | 存在不全为零的实数λ1,λ2,λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$=$\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<$\frac{1}{2}$ | B. | a≤$\frac{1}{2}$ | C. | a≤1 | D. | a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对附中的看法 | 非常好,附中推行素质教育,身心得以全面发展 | 很好,我的高中生活很快乐很充实 |
| A班人数比例 | $\frac{3}{4}$ | $\frac{1}{4}$ |
| B班人数比例 | $\frac{2}{3}$ | $\frac{1}{3}$ |
| C班人数比例 | $\frac{1}{2}$ | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com