
(本题满分16分)已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线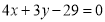 相切.
相切.
(1)求圆的标准方程;
(2)设直线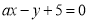
 与圆相交于
与圆相交于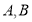 两点,求实数
两点,求实数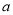 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数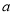 ,使得弦
,使得弦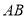 的垂直平分线
的垂直平分线 过点
过点 .
.
【解析】
试题分析:(1)设圆心为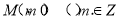 由圆与直线
由圆与直线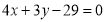 相切,根据圆心到直线的距离等于半径求出
相切,根据圆心到直线的距离等于半径求出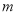 ;(2)由圆与直线相交,则圆心
;(2)由圆与直线相交,则圆心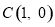 与直线
与直线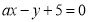 的距离小于半径;(3)若存在,设
的距离小于半径;(3)若存在,设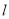 的方程为
的方程为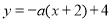 ,即
,即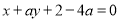 ,又因为弦
,又因为弦 的垂直平分线必过圆心,把圆心坐标代入直线方程求出实数
的垂直平分线必过圆心,把圆心坐标代入直线方程求出实数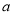 ,检验此时直线
,检验此时直线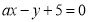
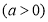 与圆相交于两点.
与圆相交于两点.
试题解析:(1)设圆心为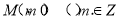
由于圆与直线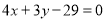 相切,且半径为5,
相切,且半径为5,
所以
即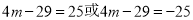 ,
,
解得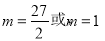
因为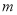 为整数,故
为整数,故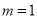 ,
,
故所求的圆的方程是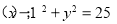 (5分)
(5分)
(2) 此时,圆心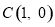 与该直线的距离
与该直线的距离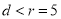
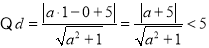
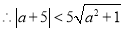
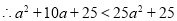
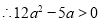 即:
即: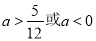 (10分)
(10分)
(2)设符合条件的实数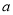 存在,
存在,
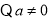 ,则直线
,则直线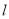 的斜率为
的斜率为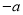 ,
,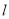 的方程为
的方程为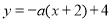 ,即
,即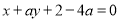 .
.
由于 垂直平分弦
垂直平分弦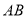 ,故圆心
,故圆心 必在
必在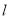 上.
上.
所以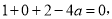 解得
解得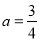 .
.
经检验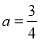 ,直线
,直线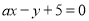 与圆有两个交点, (14分)
与圆有两个交点, (14分)
故存在实数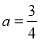 ,使得过点
,使得过点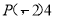 的直线
的直线 垂直平分弦
垂直平分弦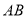 (16分)
(16分)
考点:1.圆的方程;2.直线与圆的位置关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年江西省赣州市十二县高二上学期期中联考理科数学试卷(解析版) 题型:选择题
若直线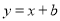 与曲线
与曲线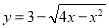 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( )
A.[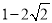 ,
,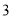 ] B.[
] B.[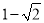 ,3]
,3]
C.[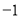 ,
,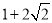 ] D.[
] D.[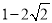 ,
,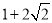 ]
]
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省淮安市高二上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分14分)在平面直角坐标系 中,已知点A(-2,1),直线
中,已知点A(-2,1),直线 .
.
(1)若直线 过点A,且与直线
过点A,且与直线 平行,求直线
平行,求直线 的方程;
的方程;
(2)若直线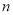 过点A,且与直线
过点A,且与直线 垂直,求直线
垂直,求直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省淮安市高二上学期期中考试数学试卷(解析版) 题型:填空题
在立体几何中,下列结论一定正确的是: (请填所有正确结论的序号)
①一般地,由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱;
②用一个平面去截棱锥,得到两个几何体,一个仍然是棱锥,另一个我们称之为棱台;
③将直角三角形绕着它的一边所在的直线旋转一周,形成的几何体叫做圆锥;
④将直角梯形绕着它的垂直于底边的腰所在的直线旋转一周,形成的几何体叫做圆台.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北长阳县第一高中高二上学期期中考试文科数学试卷(解析版) 题型:填空题
设 ABC的内角A,B,C的对边分别为
ABC的内角A,B,C的对边分别为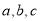 ,且
,且
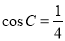 ,则
,则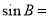 _________.
_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com