
分析 (1)根据排列数公式,化简计算,再验证即可到解集.
(2)对于题目中新定义的:“Cnx”理解是解决此题的问题,如求${C}_{8}^{\frac{3}{2}}$,它是由一个分式的分子和分母两部分构成,分子是8,分母是的分数.按此理解将函数Cx8的值域问题转化成一个函数的值域.
解答 解:(1)∵$\frac{1}{{C}_{n}^{3}}$-$\frac{1}{{C}_{n}^{4}}$<$\frac{1}{{C}_{n}^{12}}$,
∴$\frac{3!(n-3)_!}{n!}$-$\frac{4!(n-4)!}{n!}$<$\frac{12!(n-12)!}{n!}$,
∴3!(n-3)!-4!(n-4)!<12!(n-12)!,
∴3!(n-4)(n-5)…(n-11)(n-7)<12!,
∴(n-4)(n-5)…(n-11)(n-7)<2×11!,
当n=15时,(n-4)(n-5)…(n-11)(n-7)=11×10×9×8×7×6×5×4×8>2×11!,
当n=14时,(n-4)(n-5)…(n-11)(n-7)=10×9×8×7×6×5×4×3×7<2×11!,
∵n≥12,
∴n=12,13,14,
∴$\frac{1}{{C}_{n}^{3}}$-$\frac{1}{{C}_{n}^{4}}$<$\frac{1}{{C}_{n}^{12}}$的解集为{12,13,14}
(2)当x∈[$\frac{3}{2}$,2]时,${C}_{8}^{\frac{3}{2}}$=$\frac{8}{\frac{3}{2}}$=$\frac{16}{3}$,当x→2时,[x]=1,所以C8x=$\frac{8}{2}$=4,
当[2,3)时,C82=$\frac{8×7}{2×1}$=28,
当x→3时,[x]=2,C8x=$\frac{8×7}{x(x-1)}$=$\frac{56}{x(x-1)}$,
又∵当x∈[2,3)时,f(x)=x(x-1)∈[2,6),
∴$\frac{56}{x(x-1)}$∈($\frac{28}{3}$,28],
∴故C8x的值域为($\frac{16}{3}$,4]∪($\frac{28}{3}$,28].
点评 本本题是一道创新题,新的高考,每年均会出现一定新颖的题目,我们只要认真审题,细心研究,活用基础知识,把握数学思想、数学方法,构建知识结构和认知结构,实现知识到能力的转化,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
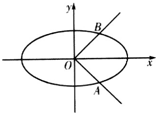 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{6}}}{3}$,点O为坐标原点,椭圆C与曲线|y|=x的交点分别为A,B(A在第四象限),且$\overrightarrow{OB}•\overrightarrow{AB}=\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$.
设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com