【题目】已知函数
，其中
.
（1）当
时，求曲线
在点
处的切线方程；
（2）当
时，求函数
的极值．
【答案】（1）
（2）当
时，极大值为1，极小值为
；当
时，极大值为1，极小值为.
【解析】
（1）利用导数的几何意义求切线方程即可；
（2）求导，分类讨论参数
的值，利用导数求出极值即可.
（1）当
时，
，
又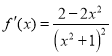
，
所以曲线
在点
处的切线方程为：
即.
（2）
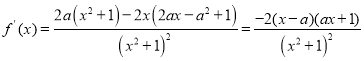
①当，令
得到
，
当
变化时，
和
的变化情况如下表：
|
|
|
|
|
|
|
| 0 |
| 0 |
|
| 极小值 | 极大值 |
所以在区间
，
内为减函数，在区间
内为增函数，所以函数的极小值为
，极大值为
.
②当时，令得
，
，
当变化时，和的变化情况如下表：
|
|
|
|
|
|
|
| 0 |
| 0 |
|
| 极大值 | 极小值 |
所以在
，
内为增函数，在
内为减函数，
所以函数的极小值为，极大值为
.
综上，当时，函数的单调递增区间为，单调递减区间为，，极大值为1，极小值为.
当时，函数的单调递增区间为，，递减区间为，极大值为1，极小值为.
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
（
）的左、右焦点分别为
，焦距为
，过点
作直线交椭圆于
两点，
的周长为
.
（1）求椭圆的方程；
（2）若斜率为
的直线
与椭圆相交于
两点，求定点
与交点所构成的三角形
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某电视台举行一个比赛类型的娱乐节目， 
两队各有六名选手参赛，将他们首轮的比赛成绩作为样本数据，绘制成茎叶图如图所示，为了增加节目的趣味性，主持人故意将
队第六位选手的成绩没有给出，并且告知大家
队的平均分比
队的平均分多4分，同时规定如果某位选手的成绩不少于21分，则获得“晋级”.
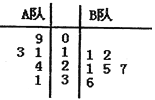
（1）根据茎叶图中的数据，求出
队第六位选手的成绩；
（2）主持人从
队所有选手成绩中随机抽2个，求至少有一个为“晋级”的概率；
（3）主持人从
两队所有选手成绩分别随机抽取2个，记抽取到“晋级”选手的总人数为
，求
的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三棱锥P﹣ABC的所有棱长为1．M是底面△ABC内部一个动点（包括边界），且M到三个侧面PAB，PBC，PAC的距离h1，h2，h3成单调递增的等差数列，记PM与AB，BC，AC所成的角分别为α，β，γ，则下列正确的是（ ）
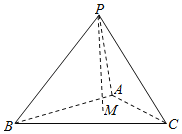
A.α＝βB.β＝γC.α＜βD.β＜γ
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，曲线
的极坐标方程为
，以极点为原点
，极轴为
轴正半轴（两坐标系取相同的单位长度）的直角坐标系
中，曲线
的参数方程为：
为参数）．
（1）求曲线的直角坐标方程与曲线的普通方程；
（2）将曲线经过伸缩变换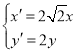
后得到曲线
，若
，
分别是曲线和曲线上的动点，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，曲线
的参数方程为
(
为参数)，以
为极点，以
轴的正半轴为极轴，建立极坐标系，直线
的极坐标方程为 
（1）求曲线的普通方程和直线的直角坐标方程；
（2）设点
，若直线与曲线相交于
，
两点，且
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一动圆P与定圆
外切，且与直线
相切，记动点P的轨迹为曲线E．
（1）求曲线E的方程；
（2）过点
作直线l与曲线E交于不同的两点B、C，设BC中点为Q，问：曲线E上是否存在一点A，使得
恒成立？如果存在，求出点A的坐标；如果不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
