练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)＝的图像如图K10­4所示，则a＋b＋c＝________．


    　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)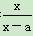＝(x≠a)．

    (1)若a＝－2，试证f(x)在区间(－∞，－2)上单调递增；

    (2)若a>0，且f(x)在区间(1，＋∞)上单调递减，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝2|x－1|的大致图像是(　　)

    图K8­2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝则不等式f(x)>1的解集为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数y＝f(x＋3)的图像经过点P(1，4)，则函数y＝f(x)的图像必经过点________．

    能力提升

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝x2－ax＋1有且仅有一个零点，则实数a的值为(　　)

    A．0  B．2或－2  C．－2  D．2

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    执行如图K11­1所示的程序框图，若输入如下四个函数：①f(x)＝2x；②f(x)＝－2x；③f(x)＝x＋x－1；④f(x)＝x－x－1.

    则输出函数的序号为(　　)

    A．①  　　　B．②

    C．③  　　　D．④

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某俱乐部为救助失学儿童，准备在某体育场举行一场足球义赛，预计卖出门票2.4万张，票价有3元、5元和8元三种，且票价为3元和5元的门票张数(单位：万张)之积为0.6.设x是门票的总收入，经计算，扣除其他各项开支后，该俱乐部的纯收入为y＝lg 2x，为了使募捐的纯收入最大，则这三种门票的张数分别为(　　)

    A．1，0.8，0.6  B．0.6，1，0.8

    C．0.6，0.8，1  D．0.8，0.6，1

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


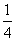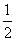    设函数f(x)＝ln x－x2－x.

    (1)求函数f(x)的极值；

    (2)若g(x)＝x(f(x)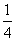＋x2＋1)，当x>1时，g(x)在区间(n，n＋1)内存在极值，求整数n的值．

     

    查看答案和解析>>

    同步练习册答案