练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．函数y=3cos（x+100）+5sin（x+40°）的最大值是7．

    分析 将x+40°化成x+10°+30°，使用差角公式展开，合并再用辅助角公式化简，得出最值即可．

    解答 解：y=3cos（x+10°）+5sin（x+40°）=3cos（x+10°）+5sin[（x+10°）+30°]
    =3cos（x+10°）+5[sin（x+10°）cos30°+cos（x+10°）sin30°]
    =3cos（x+10°）+$\frac{5\sqrt{3}}{2}$sin（x+10°）$+\frac{5}{2}$cos（x+10°）
    =$\frac{11}{2}cos（x+10°）+\frac{5\sqrt{3}}{2}sin（x+10°）$
    =7cos（x+10°+θ）．
    ∴函数y=3cos（x+100）+5sin（x+40°）的最大值是7．
    故答案为：7．

    点评 本题考查了三角函数恒等变换及求值，发现两个角的特殊关系是关键，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．如图P为平行四边形ABCD所在平面外一点，Q为PA的中点，O为AC与BD的交点，下面说法错误的是（　　） 
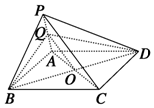
    A．OQ∥平面PCDB．PC∥平面BDQC．AQ∥平面PCDD．CD∥平面PAB

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知递增等差数列{an}满足a1•a4=7，a2+a3=8．
    （1）求数列{an}的通项公式；
    （2）设bn=$\frac{1}{{{a_n}{a_{n+1}}}}$，数列{bn}的前n项和为Sn，求证：Sn$＜\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在四边形ABCD中，∠A=90°，∠B=60°，∠D=120°，对角线AC长为4，则对角线BD的长为$\frac{8\sqrt{3}}{3}$，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知函数$f（x）=sin（{2x+\frac{π}{3}}）$，定义域为[a，b]，值域是$[{-1\;，\;\;\frac{1}{2}}]$，则下列正确命题的序号是（1）、（2）、（4）．
    （1）b-a最小值是$\frac{π}{3}$；
    （2）b-a最大值是$\frac{2π}{3}$；
    （3）b-a无最大值；
    （4）直线$x=\frac{2015}{12}π$不可能是此函数的对称轴．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．在△ABC中，若a=4，b=3，c=2，则△ABC的最小角为arccos$\frac{7}{8}$（用反三角函数表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知$0＜α＜\frac{π}{2}$，$-\frac{π}{2}＜β＜0$，$cos（{α-β}）=\frac{3}{5}$，且$tanα=\frac{3}{4}$，求$tan（{β+\frac{π}{4}}）$的值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数$f（x）=\frac{1-x}{1+x}$．
    （1）求证：$f（{\frac{1}{x}}）=-f（x）$．（x≠-1，x≠0）
    （2）说明f（x）的图象可以由函数$y=\frac{2}{x}$的图象经过怎样的变换得到？
    （3）当x∈Z时，m≤f（x）≤M恒成立，求M-m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=lnx-a（x-1），a∈R．
    （Ⅰ）求函数f（x）在（1，f（1））处的切线方程；
    （Ⅱ）当x≥1时，f（x）≤$\frac{lnx}{x+1}$恒成立，求a的取值范围；
    （Ⅲ）当x≥1时，求证：不等式ex-1-a（x2-x）≥xf（x）+1．

    查看答案和解析>>

    同步练习册答案