
分析 ①根据分布计数原理进行计算.
②根据排列组合进行计算.
③根据排列组合进行计算.
④根据二项式系数的性质进行判断.
解答 解:①乘积(a+b+c+d)(p+q+r)(m+n)展开式的项数是4×3×2=24;故①正确,
②如果5在两端,则1、2有三个位置可选,排法为2×A32A22=24种,
如果5不在两端,则1、2只有两个位置可选,首先排5,有${C}_{3}^{1}$=3种,然后排1和2,有A22A22=12种,
3×A22A22=12种,共计12+24=36种;故②正确;
③将空位插到三个人中间,三个人有两个中间位置和两个两边位置,就是将空位分为四部分,五个空位四分只有1,1,1,2
空位五差别,只需要空位2分别占在四个位置就可以有四种方法,另外三个人排列A33=6,
根据分步计数可得共有4×6=24,故③正确,;
④由(1+x)8=a0+a1x+a2x2+…+a8x8.
可知:a0,a1,a2…a8均为二项式系数,
依次是c80,c81,c82…c88.
∵C80=C88=1,C81=C87=8,C82=C86=28;C83=C85=56;C84=70
∴a0,a1,a2…a8中奇数只有a0,a8两个,故④正确,
故答案为:①②③④.
点评 本题主要考查命题的真假判断,涉及排列组合以及二项式定理的应用,考查学生的运算和推理能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
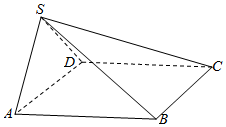 如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,平面SAD⊥平面ABCD,SA=SD=2,AB=3.
如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,平面SAD⊥平面ABCD,SA=SD=2,AB=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y=0或$\frac{x}{25}$+y=0 | B. | x-y=0或$\frac{x}{25}$+y=0 | C. | x+y=0或$\frac{x}{25}$-y=0 | D. | x-y=0或$\frac{x}{25}$-y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com