
分析 如图所示,我们研究平行直线系与函数f(x)=x2(0≤x≤1)图象的关系,其中函数图象完全在某相邻的两条平行直线l1与l2之间,图象上的个别点在直线上.
设两条平行直线l1与l2之间的距离为d.我们发现只有l1经过点O(0,0),A(1,1),l2与图象相切于点P时,H(a,b)的最小值=$\frac{1}{2}$d.求出即可得出.
解答 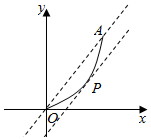 解:如图所示
解:如图所示
我们研究平行直线系与函数f(x)=x2(0≤x≤1)图象的关系,
其中函数图象完全在某相邻的两条平行直线l1与l2之间,图象上的个别点在直线上.
设两条平行直线l1与l2之间的距离为d.
我们发现只有l1经过点O(0,0),A(1,1),l2与图象相切于点P时,
H(a,b)的最小值=$\frac{1}{2}$d.
设P$({x}_{0},{x}_{0}^{2})$,f′(x)=2x.
∵kOA=1,∴2x0=1,解得x0=$\frac{1}{2}$.
∴P$(\frac{1}{2},\frac{1}{4})$,
直线OA的方程为:y=x.
∴d=$\frac{|\frac{1}{2}-\frac{1}{4}|}{\sqrt{2}}$=$\frac{\sqrt{2}}{8}$.
∴H(a,b)的最小值=$\frac{1}{2}$d=$\frac{\sqrt{2}}{16}$.
故答案为:$\frac{\sqrt{2}}{16}$.
点评 本题考查了利用导数研究曲线的切线的斜率、平行线之间的距离、点到直线的距离公式,考查了数形结合方法、推理能力与计算能力,属于难题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ${\vec e_1}$=(0,0),${\vec e_2}$=(1,2) | B. | ${\vec e_1}$=(0,-1),${\vec e_2}$=(-1,0) | ||
| C. | ${\vec e_1}$=(-2,3),${\vec e_2}$=(4,-6) | D. | ${\vec e_1}$=(1,3),${\vec e_2}$=(4,12) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{AM}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知O为坐标原点,P为双曲线$\frac{x^2}{a^2}$-y2=1(a>0)上一点,过P作两条渐近线的平行线交点分别为A,B,若平行四边形OAPB的面积为$\frac{{\sqrt{3}}}{2}$,则双曲线的离心率为( )
已知O为坐标原点,P为双曲线$\frac{x^2}{a^2}$-y2=1(a>0)上一点,过P作两条渐近线的平行线交点分别为A,B,若平行四边形OAPB的面积为$\frac{{\sqrt{3}}}{2}$,则双曲线的离心率为( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{10}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com