
���� ��1������x=��cos�ȣ���2=x2+y2��������C�ļ����귽���Ǧ�=4cos�ȣ�����ͬ�˦ѣ�����ֱ�����귽�̣�
��2�����ò����ļ������壬������|PA|+|PB|��
��� �⣺��1������C�ļ����귽���Ǧ�=4cos�ȣ����Ԧ�2=4��cos�ȣ�����ֱ�����귽���ǣ�x2+y2=4x������x-2��2+y2=4������3�֣�
��2�����A��B��Ӧ�IJ����ֱ�Ϊt1��t2����$\left\{\begin{array}{l}{x=2-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$�����루x-2��2+y2=4������${t^2}+\sqrt{2}t-3=0$����$\left\{{\begin{array}{l}{{t_1}+{t_2}=-\sqrt{2}}\\{{t_{1•}}{t_2}=-3}\end{array}}\right.$����..��5�֣�
��|PA|+|PB|=$|{t_1}|+|{t_2}|=|{{t_1}-{t_2}}|={��{t_1}+{t_2}��^2}-4{t_1}t{\;}_2=\sqrt{14}$��..��10�֣�
���� ���⿼�鼫���귽����ֱ�����귽�̵Ļ��������������������ã������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3-\sqrt{3}}{3}$ | B�� | $\frac{3}{2}$ | C�� | 1-$\sqrt{3}$ | D�� | $\sqrt{3}$-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
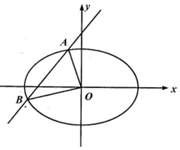 ��ͼ����б��Ϊk��k��0����ֱ��l����ԲC��$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1����A��B���㣬��OA��OB��
��ͼ����б��Ϊk��k��0����ֱ��l����ԲC��$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1����A��B���㣬��OA��OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
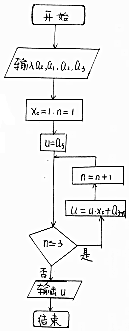 ��ͼ�����ͼ���㷨˼·��Դ���ҹ��Ŵ���ѧ��������ѧ���¡��еġ��ؾ����㷨�������ʽ��ֵ��ִ�г����ͼ��������a0=1��a1=1��a2=0��a3=-1���������u��ֵΪ��������
��ͼ�����ͼ���㷨˼·��Դ���ҹ��Ŵ���ѧ��������ѧ���¡��еġ��ؾ����㷨�������ʽ��ֵ��ִ�г����ͼ��������a0=1��a1=1��a2=0��a3=-1���������u��ֵΪ��������| A�� | 2 | B�� | 1 | C�� | 0 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ����һ������ֻ��һ��ֱ������ֱ֪��ƽ�� | |
| B�� | �����ߵ�������ȷ��һ��ƽ�� | |
| C�� | �������ֱ�ߴ�ֱ��ͬһ��ֱ�ߣ���ô������ֱ��ƽ�� | |
| D�� | �������ƽ�洹ֱ��ͬһ��ƽ�棬��ô������ƽ����ܻ��ഹֱ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x-2 | B�� | $y=\frac{{{x^2}-4}}{x+2}$ | C�� | $y=\frac{{{{��{x-2}��}^2}}}{x-2}$ | D�� | $y={��{\frac{x-2}{{\sqrt{x-2}}}}��^2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com