
| 1 |
| x |
| a1+a2+…+an |
| n |
| 1 |
| x |
| 1 |
| x |
| 1-x |
| x2 |
| 1 |
| x |
| x1 |
| x2 |
| x2 |
| x1 |
| 1 |
| x1 |
| ai |
| a1+a2+…+an |
| 1 |
| ai |
| a1 |
| a1+a2+…+an |
| a2 |
| a1+a2+…+an |
| an |
| a1+a2+…+an |
| a1 |
| a1+a2+…+an |
| 1 |
| a1 |
| a2 |
| a1+a2+…+an |
| 1 |
| a2 |
| an |
| a1+a2+…+an |
| 1 |
| an |
| n |
| a1+a2+…+an |
| a1+a2+…+an |
| n |
| a1+a2+…+an |
| n |
| a1+a2+…+an |
| n |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| x | 1 | 2 | 3 | 4 |
| y | 1 | 5-a | 3 | 7+a |
 |
| y |
 |
| b |
 |
| a |
A、(4,
| ||
B、(
| ||
| C、(6,8) | ||
D、(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
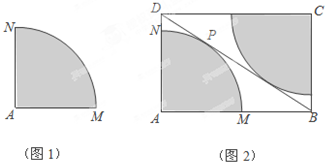 某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).
某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
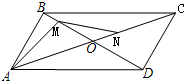 如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=
如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60°,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM=| 1 |
| 3 |
| 1 |
| 3 |
| AB |
| a |
| AD |
| b |
| a |
| b |
| MN |
| MN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com