
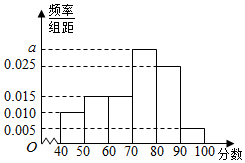
 某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).
某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).分析 (Ⅰ)根据频率分布直方图,用1减去成绩落在其它区间上的频率,即得成绩落在[70,80)上的频率.
(Ⅱ) 先根据频率分布直方图,和平均数的定义即可求出.
(Ⅲ)先求出成绩是80分以上的人数,再分别求得成绩落在区间[80,90)、[90,100]上的人数,即可求得其中恰有1人的分数不低于90分.
解答 解:(Ⅰ)分数在[70,80)内的频率为:1-(0.010+0.015+0.015+0.025+0.005)×10=1-0.7=0.3.…(2分)
(Ⅱ)平均分为:$\overline x=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71$(分). …(4分)
(Ⅲ)由题意,[80,90)分数段的人数为:0.25×60=15(人);…(5分)[90,100]分数段的人数为:0.05×60=3(人);…(6分)
因为用分层抽样的方法在8(0分)以上(含80分)的学生中抽取一个容量为6的样本,所以[80,90)分数段抽取5人,分别记为A,B,C,D,E;[90,100]分数段抽取1人,记为M. …(8分)
因为从样本中任取2人,其中恰有1人的分数不低于9(0分),
则另一人的分数一定是在[80,90)分数段,所以只需在分数段[80,90)抽取的5人中确定1人.
设“从样本中任取2人,其中恰有1人的分数不低于9(0分)为”事件A,…(9分)
则基本事件空间包含的基本事件有:(A,B),(A,C),(A,D),(A,E),
(B,C),(B,D),(B,E),(C,D),(C,E),(D,E),(A,M),(B,M),
(C,M),(D,M),(E,M)共15种.
事件A包含的基本事件有(A,M),(B,M),(C,M),(D,M),(E,M)5种…(11分)
所以恰有1人的分数不低于9(0分)的概率为$P(A)=\frac{5}{15}=\frac{1}{3}$. …(12分)
点评 本题主要考查频率分布直方图、用样本估计总体、等可能事件的概率,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:解答题
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 幂函数的图象都经过点(1,1)和点(0,0) | |
| B. | 当α=0时,函数y=xα的图象是一条直线 | |
| C. | 若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大 | |
| D. | 幂函数y=xα,当α<0时,在第一象限内函数值随x值的增大而减小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知Rt△OAB中,∠AOB=90°,OA=3,OB=2,M在OB上,且OM=1,N在OA上,且ON=1,P为AM与BN的交点,求∠MPN.(要求用向量求解).
如图,已知Rt△OAB中,∠AOB=90°,OA=3,OB=2,M在OB上,且OM=1,N在OA上,且ON=1,P为AM与BN的交点,求∠MPN.(要求用向量求解).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com