
分析 (Ⅰ)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=1,再由x=1代入椭圆方程,可得弦长,解方程可得a,b,进而得到椭圆方程;
(Ⅱ)设直线l的方程为y=kx+2,M(x1,y1),N(x2,y2),MN的中点为E(x0,y0),在x轴上假设存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形,即有AE⊥MN.将直线方程代入椭圆方程,运用韦达定理和中点坐标公式,以及两直线垂直的条件:斜率之积为-1,结合基本不等式即可得到所求m的范围,进而判断存在.
解答 解:(Ⅰ)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=1,即a2-b2=1,
又x=1时,y=±b$\sqrt{1-\frac{1}{{a}^{2}}}$,
可得$\frac{2{b}^{2}}{a}$=3,
解得a=2,b=$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)设直线l的方程为y=kx+2,M(x1,y1),N(x2,y2),MN的中点为E(x0,y0),
在x轴上假设存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形,
即有AE⊥MN,
由y=kx+2代入椭圆方程,可得(3+4k2)x2+16kx+4=0,
则△=(16k)2-16(3+4k2)>0,解得k>$\frac{1}{2}$或k<-$\frac{1}{2}$,
x1+x2=-$\frac{16k}{3+4{k}^{2}}$,中点x0=-$\frac{8k}{3+4{k}^{2}}$,
y0=k•(-$\frac{8k}{3+4{k}^{2}}$)+2=$\frac{6}{3+4{k}^{2}}$,
由kAE=-$\frac{1}{k}$,可得$\frac{\frac{6}{3+4{k}^{2}}-0}{\frac{-8k}{3+4{k}^{2}}-m}$=-$\frac{1}{k}$,
可得m=-$\frac{2k}{3+4{k}^{2}}$=$\frac{-2}{4k+\frac{3}{k}}$,
当k>$\frac{1}{2}$时,4k+$\frac{3}{k}$≥4$\sqrt{3}$,即有-$\frac{\sqrt{3}}{6}$≤m<0;
当k<-$\frac{1}{2}$时,4k+$\frac{3}{k}$≤-4$\sqrt{3}$,即有0<m≤$\frac{\sqrt{3}}{6}$.
综上可得,存在点A(m,0),且m∈[-$\frac{\sqrt{3}}{6}$,0)∪(0,$\frac{\sqrt{3}}{6}$],
使得以AM,AN为邻边的平行四边形为菱形.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质,考查存在性问题的解法,注意运用直线方程和椭圆方程联立,运用韦达定理和判别式大于0,以及中点坐标公式和两直线垂直的条件:斜率之积为-1,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 红球个数 | 3 | 2 | 1 | 0 |
| 实际付款 | 半价 | 7折 | 8折 | 原价 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,$\frac{1}{4}$) | B. | (-$\frac{1}{2}$,$\frac{1}{2}$) | C. | (-2,2) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | ($\frac{3}{2}$,+∞) | C. | (2,+∞) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
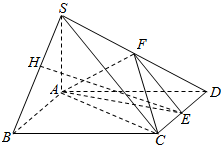 如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.
如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com