
分析 (1)任取直线l:x+y=0上一点P(x′,y′),经矩阵变换后点为P(x′,y),利用矩阵乘法得出坐标之间的关系,求出直线l′的方程;
(2)求出|A|,即可求A的逆矩阵A-1.
解答 解:(1)任取直线l:x+y=0上一点P(x′,y′),
经矩阵变换后点为P′(x,y),则有$(\begin{array}{l}{1}&{2}\\{-1}&{2}\end{array})$(x′,y′)=(x,y),
可得$\left\{\begin{array}{l}{x=x′+2y′}\\{y=-x′+2y′}\end{array}\right.$,解得$\left\{\begin{array}{l}{x′=\frac{x-y}{2}}\\{y′=\frac{x+y}{4}}\end{array}\right.$,
代入直线l:x′+y′=0,化简得3x-y=0.
直线l′的方程3x-y=0;
(2)∵矩阵A=$(\begin{array}{l}{1}&{2}\\{-1}&{2}\end{array})$,
∴|A|=1×2-2×(-1)=4,
∴A-1=$[\begin{array}{l}{\frac{1}{2}}&{-\frac{1}{2}}\\{\frac{1}{4}}&{\frac{1}{4}}\end{array}]$.
点评 本题以矩阵为依托,考查矩阵的乘法,矩阵,考查矩阵变换,关键是正确利用矩阵的乘法公式.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1±5\sqrt{2}}{7}$ | B. | $\frac{5±\sqrt{221}}{14}$ | C. | ±1 | D. | 以上A、B、C均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
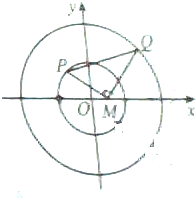 如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.
如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com