
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,且
是菱形,且![]() .
.
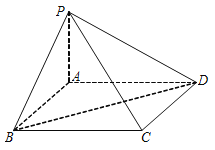
(1)求证:![]() ;
;
(2)若平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+(1﹣a) x2﹣a(a+2)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是﹣3,求a,b的值;
(2)若函数f(x)在区间(﹣1,1)上不单调,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,即
,即![]() .
.
(1)若数列![]() 为首项为2016,公比为
为首项为2016,公比为![]() 的等比数列,
的等比数列,
①求![]() 的表达式;②当
的表达式;②当![]() 为何值时,
为何值时, ![]() 取得最大值;
取得最大值;
(2)当![]() 时,数列
时,数列![]() 都有
都有![]() 且
且![]() 成立,
成立,
求证: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )
A.y=f(x)的最小正周期为π,且在(0, ![]() )上为增函数
)上为增函数
B.y=f(x)的最小正周期为π,且在(0, ![]() )上为减函数
)上为减函数
C.y=f(x)的最小正周期为 ![]() ,且在
,且在 ![]() 上为增函数
上为增函数
D.y=f(x)的最小正周期为 ![]() ,且在
,且在 ![]() 上为减函数
上为减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行围棋比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或下满6局时停止.设甲在每局中获胜的概率为p(p> ![]() ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 ![]() .
.
(1)求p的值;
(2)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F. 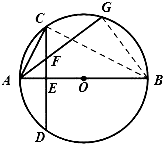
(1)求证:E、F、G、B四点共圆;
(2)若GF=2FA=4,求线段AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com