
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ڢ� |
���� �����ĵ������ֱ����ú��������Ժ͵���֮��Ĺ�ϵ�����жϼ��ɣ�
��� �⣺�����Ķ�����Ϊ��0��+�ޣ���
�����ĵ���f�䣨x��=$\frac{2k-1}{x}$-$\frac{k}{{x}^{2}}$+2=$\frac{2{x}^{2}+��2k-1��x-k}{{x}^{2}}$=$\frac{��x+k����2x-1��}{{x}^{2}}$=$\frac{2��x+k����x-\frac{1}{2}��}{{x}^{2}}$��
�ٵ�k=-$\frac{1}{2}$ʱ��f�䣨x��=$\frac{2��x-\frac{1}{2}��^{2}}{{x}^{2}}$��0�����������f��x���ڣ�0��+�ޣ��ϵ���������
���ڣ�0��$\frac{1}{2}}$���ϵ����������ʢ���ȷ��
�ڵ�k��0ʱ����f�䣨x����0��x��$\frac{1}{2}$����ʱ����Ϊ��������
��f�䣨x����0����0��x��$\frac{1}{2}$����ʱ����Ϊ������������x=$\frac{1}{2}$ʱ������f��x�����ڼ�Сֵ��
���ɺ���f��x���ڣ�0��+�ޣ����м���ֵ���ʢڴ���
�۵�-$\frac{1}{2}$��k��0ʱ����0��-k��$\frac{1}{2}$��
��f�䣨x����0��-k��x��$\frac{1}{2}$��
��f�䣨x����0��0��x��-k��x��$\frac{1}{2}$��������f��x���ڣ�$\frac{1}{2}$��+�ޣ��ϵ����������ʢ۴���
�ܵ�k��-$\frac{1}{2}$ʱ��-k��$\frac{1}{2}$����f�䣨x����0��0��x��$\frac{1}{2}$��x��-k����ʱ��������������
��f�䣨x����0��$\frac{1}{2}$��x��-k��������Ϊ��������
������f��x���ڣ�0��+�ޣ����м���ֵf��${\frac{1}{2}}$�����м�Сֵf��-k�����ʢ���ȷ��
�ʲ���ȷ�������Ţڢۣ�
��ѡ��B
���� ������Ҫ�������������жϣ��漰�����ĵ����Ժ͵����Ĺ�ϵ������ѧ���ļ���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 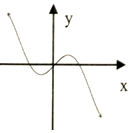 | B�� |  | C�� | 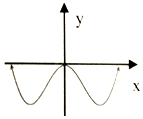 | D�� | 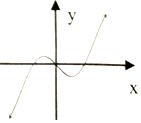 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ڶ��������� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | am+1��am+2 | B�� | am+1��bm+2 | C�� | bm+2��am+2 | D�� | bm+1��bm+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com