
分析 作出不等式组 $\left\{\begin{array}{l}x+y≥1\\ x-2y≤4\end{array}\right.$的表示的区域D,根据线性规划的应用结合特称命题和全称命题的定义和性质对四个选项逐一分析即可.
解答 解:作出不等式组$\left\{\begin{array}{l}x+y≥1\\ x-2y≤4\end{array}\right.$表示的区域: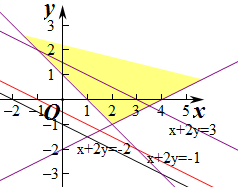
由图知,区域D为直线x+y=1与x-2y=4相交的上部角型区域,
显然,区域D所有的部分都在x+2y=-2的上方,故p1:?(x,y)∈D,x+2y≥-2成立;
故p1正确,p2错误,
区域D有一部分在x+2y=3的下方,故p3:?(x,y)∈D,x+2y≤3正确,
区域D全部在x+2y=-1的上方,故p4:?(x,y)∈D,x+2y≤-1错误.
综上所述p1,p2正确,
故答案为:p1,p2
点评 本题考查命题的真假判断与应用,利用线性规划的应用,结合数形结合是解决本题的关键.考查学生的运算和推理能力.


科目:高中数学 来源: 题型:选择题
| A. | [1-$\sqrt{2}$,1+$\sqrt{2}$] | B. | [1-$\sqrt{2}$,3] | C. | [1-2$\sqrt{2}$,3] | D. | [-1,1+$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14或-6 | B. | 12或-8 | C. | 8或-12 | D. | 6或-14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com