
【题目】选修4-4:坐标系与参数方程
已知直线L:![]() (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数)
为参数)
(Ⅰ)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(Ⅱ)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 距离的最小值.
距离的最小值.
【答案】(1)![]() (2)
(2) ![]()
【解析】
(I)把直线与曲线化为直角坐标方程,将直线l与曲线C1联立,即可得到交点坐标,然后利用两点间的距离公式即可求出|AB|.
(II)根据伸缩变换得到曲线![]() 的参数方程,设曲线C2任意点P的坐标,利用点到直线的距离公式P到直线的距离d,分子合并后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,与分母约分化简后,根据正弦函数的值域可得正弦函数的最小值,进而得到距离d的最小值即可.
的参数方程,设曲线C2任意点P的坐标,利用点到直线的距离公式P到直线的距离d,分子合并后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,与分母约分化简后,根据正弦函数的值域可得正弦函数的最小值,进而得到距离d的最小值即可.
(I)直线的普通方程为![]() ,
,![]() 的普通方程
的普通方程![]() .
.
联立方程组![]() ,解得
,解得![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() ;
;
(Ⅱ)曲线![]() 的参数方程为
的参数方程为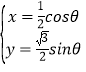 (
(![]() 为参数),故点
为参数),故点![]() 的坐标为
的坐标为![]() ,
,
从而点![]() 到直线
到直线![]() 的距离是
的距离是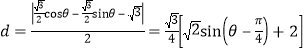
由此当![]() 时,
时,![]() 取得最小值,且最小值为
取得最小值,且最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() ,圆
,圆![]() 的方程为
的方程为![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 能否作一条直线
能否作一条直线![]() ,与点
,与点![]() 的轨迹交于
的轨迹交于![]() 两点,且点
两点,且点![]() 为线段
为线段![]() 的中点?若存在,求出直线
的中点?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·武汉六中]袋子中有四个小球,分别写有“武、汉、军、运”四个字,从中任取一个小球,有放回抽取,直到取到“军”“运”二字就停止,用随机模拟的方法估计恰好在第三次停止的概率:利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“军、运、武、汉”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下16组随机数:
232 321 230 023 123 021 132 220
231 130 133 231 331 320 122 233
由此可以估计,恰好第三次就停止的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(-3,0),Q、P分别是x轴、y轴上的动点,且使MP⊥PQ,点N在直线PQ上,![]()
(1)求动点N的轨迹C的方程.
(2)过点T(-1,0)作直线l与轨迹C交于两点A、B,问:在x轴上是否存在一点D,使△ABD为等边三角形;若存在,试求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在二项式![]() 的展开式中,
的展开式中,
(1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(最后结果用算式表达,不用计算出数值)
(2)若展开式前三项的二项式系数的和等于79,求展开式中系数最大的项.(最后结果用算式表达,不用计算出数值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com