练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个口袋内有3个不同的红球，4个不同的白球

    （1）从中任取3个球，红球的个数不比白球少的取法有多少种？

    （2）若取一个红球记2分，取一个白球记1分，从中任取4个球，使总分不少于6分的取法有多少种？

    【答案】(1) ；(2) .

    【解析】

    (1)由题意可以分类，红球个，红球个和白球个，根据计数原理即可得到答案.

    (2)从中任取个球，使总分不少于6分情况有：红球个和白球个，红球个和白球个，根据计数原理即可得到答案.

    解:(1 )从中任取个球，红球的个数不比白球少的取法：红球个，红球个和白球个.

    当取红球个时，取法有种；

    当取红球个和白球个时，.取法有种.

    根据分类计数原理,红球的个数不少于白球的个数的取法有种.

    (2 )使总分不少于分情况有两种：红球个和白球个，红球个和白球个.

    第一种，红球个和白球个，取法有种;

    第二种，红球个和白球个，取法有种,

    根据分类计数原理，使总分不少于分的取法有种.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆（为坐标原点），直线.

    （1）过直线上任意一点作圆的两条切线，切点分别为，求四边形面积的最小值.

    （2）过点的直线分别与圆交于点（不与重合），若，试问直线是否过定点？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某多面体的三视图如图所示，其中俯视图是等腰三角形，该多面体的各个面中有若干个是等腰三角形，这些等腰三角形的面积之和为______________________

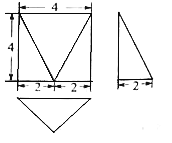
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为、，是椭圆上一动点（与左、右顶点不重合）.已知的面积的最大值为，椭圆的离心率为.

    （1）求椭圆的方程；

    （2）过的直线交椭圆于、两点，过作轴的垂线交椭圆与另一点（不与、重合）.设的外心为，求证为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）求该函数的单调区间；

    （2）若当x∈[﹣2，2]时，不等式f（x）＜m恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学拟在高一下学期开设游泳选修课，为了了解高一学生喜欢游泳是否与性别有关，该学校对100名高一新生进行了问卷调查，得到如下列联表：

    喜欢游泳

    不喜欢游泳

    合计

    男生

    10

    女生

    20

    合计

    已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为．

    （1）请将上述列联表补充完整；

    （2）并判断是否有99.9%的把握认为喜欢游泳与性别有关？并说明你的理由；

    （3）已知在被调查的学生中有5名来自甲班，其中3名喜欢游泳，现从这5名学生中随机抽取2人，求恰好有1人喜欢游泳的概率．

    下面的临界值表仅供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式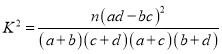：，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝.

    (1) 若不等式k≤xf(x)＋在x∈[1，3]上恒成立，求实数k的取值范围；

    (2) 当x∈ (m>0，n>0)时，函数g(x)＝tf(x)＋1(t≥0)的值域为[2－3m，2－3n]，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 a ∈ N+ ， a ≥ 2 ， 集合.在闭区间[ 1， a ] 上是否存在 b ， 使 A ∩ B ≠ ? 如果存在， 求出 b 的一切可能值及相应的 A ∩ B；如果不存在， 试说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，.

    （1）求函数的单调区间；

    （2）讨论函数的零点个数

    查看答案和解析>>

    同步练习册答案