(1)在区间[1.5]和[2.4]上分别任取一个整数.记为a.b.则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为多少?(2)在区间[1.5]和[2.4]上分别任取一个实数.记为a.b.则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

7．（1）在区间[1，5]和[2，4]上分别任取一个整数，记为a，b，则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为多少？
（2）在区间[1，5]和[2，4]上分别任取一个实数，记为a，b，则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为多少？

分析（1）先求出区间[1，5]和[2，4]上分别任取一个整数的总的事件总数，再求出满足条件的基本事件的个数，根据概率公式即可求出，
（2）如图，求出矩形的面积为8，阴影部分的面积为$\frac{15}{4}$，根据概率公式计算即可．

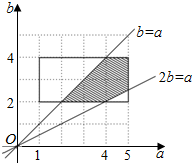解答解：（1）a可取1，2，3，4，5，b可取2，3，4，故可以构成15个曲线方程，又$\left\{\begin{array}{l}a＞b\\ \frac{{\sqrt{{a^2}-{b^2}}}}{a}＜\frac{{\sqrt{3}}}{2}\end{array}\right.$
即$\left\{\begin{array}{l}a＞b\\ \frac{b}{a}＞\frac{1}{2}\end{array}\right.$，则$\left\{\begin{array}{l}a=3\\ b=2\end{array}\right.或\left\{\begin{array}{l}a=4\\ b=3\end{array}\right.或\left\{\begin{array}{l}a=5\\ b=3\end{array}\right.或\left\{\begin{array}{l}a=5\\ b=4\end{array}\right.$，故P=$\frac{4}{15}$；
（2）如图，a，b可构成矩形，
又$\left\{\begin{array}{l}a＞b\\ \frac{b}{a}＞\frac{1}{2}\end{array}\right.$，即$\left\{\begin{array}{l}a＞b\\ 2b＞a\end{array}\right.$，即阴影区域，
则$P=\frac{S_阴}{{{S_{矩形}}}}=\frac{{\frac{15}{4}}}{8}=\frac{15}{32}$．

点评本题考查了几何概型公式的运用，几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据公式解答．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

1．已知函数f（x）=|2x-1|+|x+1|-a的图象与x轴有且仅有一个交点．
（1）求实数a的值；
（2）若m，n∈[-a，a]，求证：2|m+n|＜|4+mn|

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

2．计算：$\frac{tan68°+tan52°}{1-tan68°tan52°}$=$-\sqrt{3}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．

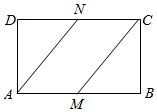如图在长方形ABCD中，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，N$是CD的中点，M是线段AB上的点，$|{\overrightarrow a}|=2，|{\overrightarrow b}|=1$．
（1）若M是AB的中点，求证：$\overrightarrow{AN}$与$\overrightarrow{CM}$共线；
（2）在线段AB上是否存在点M，使得$\overrightarrow{BD}$与$\overrightarrow{CM}$垂直？若不存在请说明理由，若存在请求出M点的位置；
（3）若动点P在长方形ABCD上运动，试求$\overrightarrow{AP}•\overrightarrow{AB}$的最大值及取得最大值时P点的位置．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

2．设函数$f（x）=\left\{\begin{array}{l}{2^{-x}}，x＜1\\{log_4}x，x＞1\end{array}\right.$，满足$f（x）=\frac{1}{4}$的x的值是$\sqrt{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

12．求值：log₂3•log₅7•log₃5•log₇4=2．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

19．设t=2x+y，其中x，y满足$\left\{\begin{array}{l}x+y-2≥0\\ x-2y+4≥0\\ 2x-y-4≤0\end{array}\right.$，则t的最大值为12．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

16．在等差数列{a_n}中，已知a₄+a₇=16，则该数列前11项和S₁₁=（　　）