
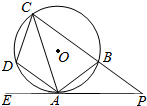
 如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.
如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.分析 (1)由弦切角定理得∠ACB=∠PAB=25°,从而∠ABC=65°,由此利用四边形ABCD内接于⊙O,能求出∠D.
(2)由∠DAE=25°,∠ACD=∠PAB,∠D=∠PBA,从而△ADC∽△PBA,由此能证明DA2=DC•BP.
解答 解:(1)∵EP与⊙O相切于点A,∴∠ACB=∠PAB=25°,
又BC是⊙O的直径,∴∠ABC=65°,
∵四边形ABCD内接于⊙O,∴∠ABC+∠D=180°,
∴∠D=115°.
证明:(2)∵∠DAE=25°,∴∠ACD=∠PAB,∠D=∠PBA,
∴△ADC∽△PBA,∴$\frac{DA}{BP}=\frac{DC}{BA}$,
又DA=BA,∴DA2=DC•BP.
点评 本题考查角的大小的求法,考查一线段平方是另两线段乘积的证明,是中档题,解题时要认真审题,注意弦切角定理的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
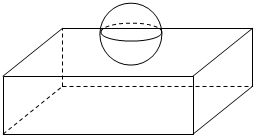 “80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R:
“80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
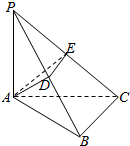 如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
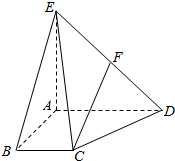 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
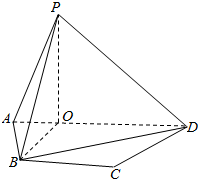 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
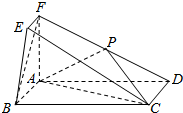 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com