
| 2max{an+1,2} |
| an |
| 8 |
| a |
| 2max{an+1,2} |
| an |
| 1 |
| a |
| 4 |
| a |
| 4 |
| a |
| 8 |
| a |
| a |
| 4 |
| 8 |
| a |
| a |
| 8 |
| 1 |
| 4 |
| 1 |
| a |
| 4 |
| a |
| 8 |
| a |
| 2max{an+1,2} |
| an |
| 1 |
| a |
| 4 |
| a |
| 4 |
| a |
| a |
| 4 |
| 1 |
| 4 |
| 1 |
| 2a |
| 1 |
| a |
| 4 |
| a |
| 4 |
| a |
| 4 |
| a |


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若m∥α,n∥β,α∥β,则m∥n |
| B、若m∥α,n∥β,α⊥β,则m⊥n |
| C、若m⊥α,n⊥β,α⊥β,则m∥n |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:
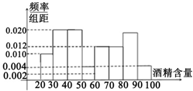 道路安全交通法规定,驾驶员血液酒精含量在20~80mg/100ml,属酒后驾车,血液酒精含量在80mg/100ml以上时,属醉酒驾车,2011年6月1日7:00至22:30,某地查处酒后驾车和醉酒驾车共50起,如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数大约为( )
道路安全交通法规定,驾驶员血液酒精含量在20~80mg/100ml,属酒后驾车,血液酒精含量在80mg/100ml以上时,属醉酒驾车,2011年6月1日7:00至22:30,某地查处酒后驾车和醉酒驾车共50起,如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数大约为( )| A、9 | B、10 | C、11 | D、12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| A、(-11,-3) |
| B、(-6,-4) |
| C、(-11,3) |
| D、(-16,-8) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知椭圆Γ:
如图,已知椭圆Γ:| x2 |
| b2 |
| y2 |
| a2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com