
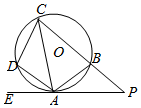
 如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长线于P,∠PAB=35°.
如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长线于P,∠PAB=35°.分析 (1)由弦切角定理得∠ACB=∠PAB=25°,从而∠ABC=65°,由此利用四边形ABCD内接于⊙O,能求出∠D.
(2)由∠DAE=25°,∠ACD=∠PAB,∠D=∠PBA,从而△ADC∽△PBA,由此能证明DA2=DC•BP,AP2=PC•BP,即可证明结论.
解答 (1)解:∵EP与⊙O相切于点A,∴∠ACB=∠PAB=35°,
又BC是⊙O的直径,∴∠ABC=55°.
∵四边形ABCD内接于⊙O,∴∠ABC+∠D=180°,
∴∠D=112°.
(2)证明:∵∠DAE=35°,
∴∠ACD=∠PAB,∠D=∠PBA,
∴△ADC∽△ABP,
∴$\frac{DA}{BP}$=$\frac{DC}{BA}$,∠DBA=∠BDA,
∴DA=BA,∴DA2=DC•BP,AP2=PC•BP,
∴$\frac{D{A}^{2}}{A{P}^{2}}$=$\frac{DC}{PC}$.
点评 本题考查角的大小的求法,考查三角形相似的判定与性质,是中档题,解题时要认真审题,注意弦切角定理的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
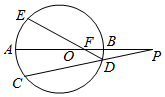 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上的一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上的一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
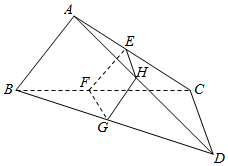 三棱锥A-BCD中,BC⊥CD,AB⊥AC,∠ABC=60°,BC=CD=2,点E,F,G分别是棱AC,BC,BD的中点,直线AD与平面EFG的交点为H.
三棱锥A-BCD中,BC⊥CD,AB⊥AC,∠ABC=60°,BC=CD=2,点E,F,G分别是棱AC,BC,BD的中点,直线AD与平面EFG的交点为H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 08 | B. | 25 | C. | 41 | D. | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com