
分析 函数h(x)=f(f(x))-1的零点个数可化为方程f(f(x))=1的解的个数,解方程f(f(x))=1即可.
解答 解:函数h(x)=f(f(x))-1的零点个数可化为
方程f(f(x))=1的解的个数,
由|lgf(x)|=1解得,
f(x)=10或f(x)=$\frac{1}{10}$;
由2|f(x)|=1得,
f(x)=0;
由f(x)=10解得,x=1010或x=$\frac{1}{1{0}^{10}}$或x=-log210;
由f(x)=$\frac{1}{10}$解得,
x=$\root{10}{10}$或x=$\frac{1}{\root{10}{10}}$;
由f(x)=0解得,x=1;
故函数h(x)=f(f(x))-1的零点个数为6;
故答案为:6.
点评 本题考查了分段函数的应用及函数的零点与方程的根的关系应用,属于基础题.


科目:高中数学 来源:2017届河北沧州一中高三上第七周周测数学试卷(解析版) 题型:解答题
如图,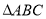 中,三个内角
中,三个内角 成等差数列,且
成等差数列,且 .
.

(1)求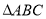 的面积;
的面积;
(2)已知平面直角坐标系 ,点
,点 ,若函数
,若函数 的图象经过
的图象经过 三点,且
三点,且 为
为 的图象与
的图象与 轴相邻的两个交点,求
轴相邻的两个交点,求 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 只有减区间没有增区间 | B. | [-1,1]是f(x)的增区间 | ||
| C. | m=±1 | D. | 最小值为-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,2,3} | C. | {3,5,9} | D. | {2,3,4,5,6,7,8,9} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com