
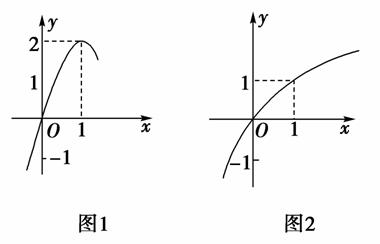
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
(1)分别求出函数f(x)和g(x)的解析式;
(2)如果函数y=g[f(x)]在区间[1,m)上单调递减,求m的取值范围.
(1)由图1得,二次函数f(x)的顶点坐标为(1,2),故可设函数f(x)=a(x-1)2+2,
又函数f(x)的图象过点(0,0),故a=-2,
整理得f(x)=-2x2+4x.
由图2得,函数g(x)=loga(x+b)的图象过点(0,0)和(1,1),
故有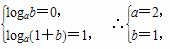
∴g(x)=log2(x+1)(x>-1).
(2)由(1)得y=g[f(x)]=log2(-2x2+4x+1)是由y=log2t和t=-2x2+4x+1复合而成的函数,而y=log2t在定义域上单调递增,要使函数y=g[f(x)]在区间[1,m)上单调递减,必须t=-2x2+4x+1在区间[1,m)上单调递减,且有t>0恒成立.
由t=0得x=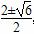 ,又t的图象的对称轴为x=1.
,又t的图象的对称轴为x=1.
所以满足条件的m的取值范围为1<m≤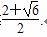 .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
已知一元二次不等式f(x)<0的解集为{x|x<-1或x>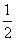 },则f(10x)>0的解集为( )
},则f(10x)>0的解集为( )
A.{x|x<-1或x>-lg2} B.{x|-1<x<-lg2}
C.{x|x>-lg2} D.{x|x<-lg2}
查看答案和解析>>
科目:高中数学 来源: 题型:
我们定义若函数f(x)为D上的凹函数须满足以下两条规则:(1)函数在区间D上的任何取值有意义;(2)对于区间D上的任意n个值x1,x2,…,xn,总满足f(x1)+f(x2)+…+f(xn)≥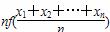 ,那么下列四个图像中在[0,
,那么下列四个图像中在[0,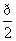 ]上满足凹函数定义的是( )
]上满足凹函数定义的是( )
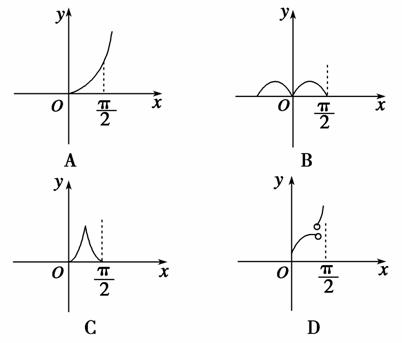
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8,设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.16 B.-16
C.a2-2a-16 D.a2+2a-16
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:关于x的函数y=x2-3ax+4在[1,+∞)上是增函数,命题q:函数y=(2a-1)x为减函数,若“p且q”为真命题,则实数a的取值范围是( )
A.(-∞,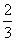 ] B.(0,
] B.(0,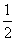 )
)
C.(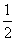 ,
,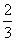 ] D.(
] D.(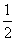 ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间( )
A.(a,b)和(b,c)内
B.(-∞,a)和(a,b)内
C.(b,c)和(c,+∞)内
D.(-∞,a)和(c,+∞)内
查看答案和解析>>
科目:高中数学 来源: 题型:
2010年7月1日某人到银行存入一年期款a元,若年利率为x,按复利计算,则到2015年7月1日可取款( )
A.a(1+x)5元 B.a(1+x)6元
C.a+(1+x)5元 D.a(1+x5)元
查看答案和解析>>
科目:高中数学 来源: 题型:
已知α为锐角,且2tan(π-α)-3cos( +β)+5=0,tan(π+α)+6sin(π+β)=1,则sinα的值是( )
+β)+5=0,tan(π+α)+6sin(π+β)=1,则sinα的值是( )
A.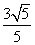 B.
B.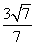
C. D.
D.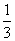
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com