
分析 (Ⅰ)利用正弦定理把已知的等式化边为角,把C用π-(A+B)表示后整理求得B的值;
(Ⅱ)利用三角函数的积化和差变形,代入角B的值,然后根据A-C的范围得答案.
解答 解:(Ⅰ)由a,b,c成等差数列,可得2b=a+c,sinA+sinC=$\sqrt{3}$,可得A+C>90°.
可得2b(sinA+sinC)=$\sqrt{3}$(a+c),
得4RsinB(sinA+AcosC)=2$\sqrt{3}$R(sinA+sinC),
即sinB=$\frac{\sqrt{3}}{2}$.
∵0°<B<180°,
∴B=60°;
(Ⅱ)∵B=60°,
∴4sinAcosC=2[sin(A+C)+sin(A-C)]
=2sin60°+2sin(A-C)
=$\sqrt{3}$+2sin(A-C).
由0°<A<120°,0°<C<120°,得
-120°<A-C<120°.
∴-1≤sin(A-C)≤1.
-2≤2sin(A-C)≤2.
∴sinAcosC的取值范围是:[$\sqrt{3}$-2,2+$\sqrt{3}$].
点评 本题考查了解三角形,训练了正弦定理的应用,考查了三角函数的积化和差公式,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
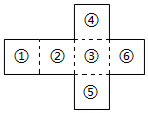 如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)
如图是一个正方体纸盒的展开图,把复数1,-1,2i,-2i,$\sqrt{2}$,-$\sqrt{2}$按虚线分别填入六个正方折成正方体后,相对面上的两个数的模相等,则不同的填法有48种(用数字作答)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
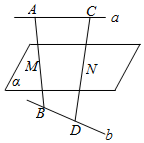 如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.
如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,-2) | B. | (1,2) | C. | (1,-2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| (49.5,59.5) | 12 | 0.24 |
| (59.5,69.5) | 16 | 0.32 |
| (69.5,79.5) | 10 | |
| (79.5,89.5) | 0.16 | |
| (89.5,99.5) | ||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com