
| A. | 99 | B. | 100 | C. | -55 | D. | 98 |
分析 由等差数列的通项公式及前n项和公式求得an=3n-23,Sn=$\frac{3{n}^{2}}{2}$-$\frac{43n}{2}$,由a8>0,a7<0,因此|a1|+|a2|+|a3|+…+|a11|=S11-2S7,代入即可求得|a1|+|a2|+|a3|+…+|a11|的值.
解答 解:由a1=-20,公差d=3,
∴an=a1+(n-1)d=3n-23,
前n项和Sn=$\frac{(-20+3n-23)×n}{2}$=$\frac{3{n}^{2}}{2}$-$\frac{43n}{2}$,
令an=0,即3n-23=0,解得:n=$\frac{23}{3}$,
∵n∈N*,
∴a8>0,a7<0,
∴|a1|+|a2|+|a3|+…+|a11|=S11-2S7=$\frac{3×1{1}^{2}}{2}$-$\frac{43×11}{2}$-2($\frac{3×{7}^{3}}{2}$-$\frac{43×7}{2}$)=99,
故选A.
点评 本题考查等差数列通项公式及前n项和公式,考查含绝对值的数列的前n项和的求法,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
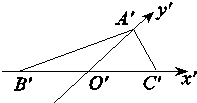 已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=$\frac{\sqrt{3}}{2}$,那么原△ABC中∠ABC的大小是( )
已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=$\frac{\sqrt{3}}{2}$,那么原△ABC中∠ABC的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | ( $\sqrt{2}$,2) | C. | (2,4) | D. | (2,2 $\sqrt{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com