练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若向量$\overrightarrow{BA}$=（1，2），$\overrightarrow{CA}$=（4，5），且$\overrightarrow{CB}$•（λ$\overrightarrow{BA}$+$\overrightarrow{CA}$）=0，则实数λ的值为（　　）
    A．3B．-$\frac{9}{2}$C．-3D．-$\frac{5}{3}$

    分析 根据平面向量的坐标运算法则与数量积运算，列出方程即可求出实数λ的值．

    解答 解：向量$\overrightarrow{BA}$=（1，2），$\overrightarrow{CA}$=（4，5），
    所以$\overrightarrow{CB}$=$\overrightarrow{CA}$+$\overrightarrow{AB}$=$\overrightarrow{CA}$-$\overrightarrow{BA}$=（3，3），
    λ$\overrightarrow{BA}$+$\overrightarrow{CA}$=（λ+4，2λ+5），
    又且$\overrightarrow{CB}$•（λ$\overrightarrow{BA}$+$\overrightarrow{CA}$）=0，
    所以3（λ+4）+3（2λ+5）=0，
    解得λ=-3．
    故选：C．

    点评 本题考查了平面向量的坐标运算与数量积运算的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．设实数x，y满足$\left\{{\begin{array}{l}{x+y-4≤0}\\{x-y≥0}\\{y≥-1}\end{array}}\right.$，则z=2x+y的最大值与最小值的和为（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知向量$\overrightarrow a$=（2，m+1），$\overrightarrow b$=（m+3，4），且（$\overrightarrow a+\overrightarrow b}$）∥（${\overrightarrow a-\overrightarrow b}$），则m=（　　）
    A．1B．5C．1或-5D．-5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$，且|$\overrightarrow a$+2$\overrightarrow b}$|=2$\sqrt{3}$，|${\overrightarrow b}$|=1，则|$\overrightarrow a}$|=（　　）
    A．1B．$\sqrt{3}$C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设a，b表示不同的直线，α，β表示不同的平面，则下列说法正确的是（　　）
    A．若a∥α，b∥β，α∥β，则a∥b
    B．若a∥α，b∥β，a∥b，则α∥β
    C．若a，b是异面直线，a∥α，b∥β，a?β，b?α，则α∥β
    D．若a，b是异面直线，a∥α，b∥β，a?β，b?α，则α∥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

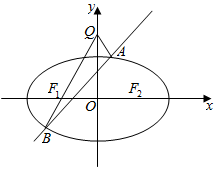    5．如图，点F1，F2分别为椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，椭圆E上任意一点到左焦点的距离的取值范围为[2-$\sqrt{2}$，2+$\sqrt{2}$]，直线l：y=kx+1与椭圆相交于A，B两点．
    （Ⅰ）求椭圆E的标准方程；
    （Ⅱ）若Q（0，2），是否存在实数k，使得△ABQ的面积为$\frac{4}{3}$？若存在，请求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知复数z=$\frac{1+i}{1+2i}$（i为虚数单位），则（　　）
    A．z的实部为$-\frac{1}{5}$B．z的虚部为$-\frac{1}{5}i$
    C．$|z|=\frac{3}{5}$D．z的共轭复数为$\frac{3}{5}+\frac{1}{5}i$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知偶函数y（x）的定义域为R，且在（0，+∞）上单调递增，则下列成立的是（　　）
    A．f（-$\frac{1}{2}$）＞f（a2+a+1）B．f（-$\frac{1}{2}$）≤f（a2+a+1）C．f（-$\frac{1}{2}$）≥f（a2+a+1）D．f（-$\frac{1}{2}$）＜f（a2+a+1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在平面直角坐标系中．直线l的参数方程为$\left\{\begin{array}{l}{x=-5+\frac{\sqrt{2}}{2}t}\\{y=-1+\frac{\sqrt{2}}{2}t}\end{array}\right.$（其中t为参数），现以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρ=4cosθ．
    （1）写出直线l和曲线C的普通方程；
    （2）已知点P为曲线C上的动点，求P到直线l的距离的最大值．

    查看答案和解析>>

    同步练习册答案