
分析 (1)椭圆C的方程为:$\frac{{x}^{2}}{{a}^{2}+1}$+$\frac{{y}^{2}}{a}$=1(a>0),可得e=$\frac{c}{a}$=$\sqrt{1-\frac{a}{{a}^{2}+1}}$=$\sqrt{1-\frac{1}{a+\frac{1}{a}}}$,利用基本不等式的性质即可得出.
(2)由椭圆的方程:$\frac{{x}^{2}}{2}$+y2=1.取特殊的相互垂直的切线:x=±$\sqrt{2}$,y=1,相交于点(±$\sqrt{2}$,1),取圆的方程:x2+y2=3.设P(x0,y0)为圆上的任意一点,则经过点P的圆的切线方程为:y-y0=k(x-x0),与椭圆方程联立化为:(1+2k2)x2+4k(y0-kx0)x+$2({y}_{0}-k{x}_{0})^{2}$-2=0,利用△=0 及其根与系数的关系即可得出.
解答 解:(1)∵椭圆C的方程为:$\frac{{x}^{2}}{{a}^{2}+1}$+$\frac{{y}^{2}}{a}$=1(a>0),∴e=$\frac{c}{a}$=$\sqrt{1-\frac{a}{{a}^{2}+1}}$=$\sqrt{1-\frac{1}{a+\frac{1}{a}}}$≥$\frac{\sqrt{2}}{2}$,当且仅当a=1设取等号,
可得椭圆的标准方程为:$\frac{{x}^{2}}{2}$+y2=1.
此时椭圆C的形状最圆.
(2)由椭圆的方程:$\frac{{x}^{2}}{2}$+y2=1.取两条特殊的相互垂直的切线:x=±$\sqrt{2}$,y=1,相交于点(±$\sqrt{2}$,1),
取圆的方程:x2+y2=3.
设P(x0,y0)为圆上的任意一点,则经过点P的圆的切线方程为:y-y0=k(x-x0),
联立$\left\{\begin{array}{l}{y-{y}_{0}=k(x-{x}_{0})}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,化为:(1+2k2)x2+4k(y0-kx0)x+$2({y}_{0}-k{x}_{0})^{2}$-2=0,
∴△=$16{k}^{2}({y}_{0}-k{x}_{0})^{2}$-8(1+2k2)$[({y}_{0}-k{x}_{0})^{2}-1]$=0,
化为:$(2-{x}_{0}^{2})$k2+2kx0y0+1-${y}_{0}^{2}$=0,$({x}_{0}^{2}≠2)$,
∴k1k2=$\frac{1-{y}_{0}^{2}}{2-{x}_{0}^{2}}$,
∵${x}_{0}^{2}$+${y}_{0}^{2}$=3,可得$1-{y}_{0}^{2}$=${x}_{0}^{2}$-2,
∴k1k2=$\frac{1-{y}_{0}^{2}}{2-{x}_{0}^{2}}$=-1.
综上可得:点M在一个定圆上x2+y2=3上.
点评 本题考查了标准方程及其性质、直线与椭圆相切问题转化为一元二次方程的实数根与判别式的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
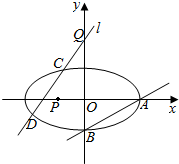 已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.
已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
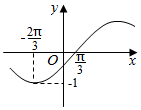 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
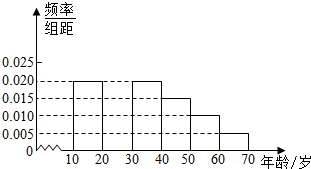 某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间调查,这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”否则称为“亚健康族”)人数及相应频率,得到统计表如图所示
某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间调查,这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”否则称为“亚健康族”)人数及相应频率,得到统计表如图所示 | 组数 | 分组 | 亚健康族的人数 | 占本组的频率 |
| 第一组 | [10,20) | 100 | 0.5 |
| 第二组 | [20,30) | 195 | P |
| 第三组 | [30,40) | 120 | 0.6 |
| 第四组 | [40,50) | a | 0.4 |
| 第五组 | [50,60) | 30 | 0.3 |
| 第六组 | [60,70] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com